题目内容
将7个红球，6个白球（小球只有颜色的区别）放入5个不同盒子，要求每个盒子中至少红球、白球各一个，则不同的放法共有（ ）
| A、20种 | B、25种 |
| C、45种 | D、75种 |
考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：根据题意，依次分析红球、白球：易得白球有C51=5种情况，7个红球放入到5个不同的盒子里，先将7个球分为5组，有2、2、1、1、1与3、1、1、1、1两种分法，故分两种情况讨论，可得黑球有15种放法，由分步计数原理，计算可得答案．
解答：
解：6个白球，放入到5个不同的盒子里，需要其中一个盒子放两个，有C51=5种情况，
7个红球放入到5个不同的盒子里，先将7个球分为5组，有2、2、1、1、1与3、1、1、1、1两种分法，若按2、2、1、1、1放入，有C52=10种放法，若按3、1、1、1、1放入，有C51=5种放法，共有15种，
则三种颜色的球有5×15=75种放法；
故选：D．
7个红球放入到5个不同的盒子里，先将7个球分为5组，有2、2、1、1、1与3、1、1、1、1两种分法，若按2、2、1、1、1放入，有C52=10种放法，若按3、1、1、1、1放入，有C51=5种放法，共有15种，
则三种颜色的球有5×15=75种放法；
故选：D．
点评：本题考查排列、组合的运用，注意本题中同色的球是相同的．
练习册系列答案
相关题目
已知椭圆C：
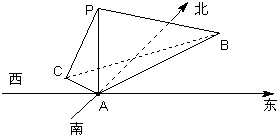在海岛A上有一座海拔1千米的山，山顶设有一个观察站P，上午9时测得一轮船在海岛北偏东30°，俯角为30°的B处，匀速直行10分钟后，测得该船位于海岛北偏西60°，俯角为45°的C处．从C处开始，该船航向改为正南方向，且速度大小不变，则该船经过10分钟后离开A点的距离为（ ）| A、1千米 | ||
| B、2千米 | ||
C、
| ||
D、2
|
某校1000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示．规定90分为优秀等级，则该校学生优秀等级的人数是（ ）| A、300 | B、150 |
| C、30 | D、15 |
函数f（x）=2x-3x的零点所在的一个区间是（ ）
| A、（-2，-1） |
| B、（-1，0） |
| C、（1，2） |
| D、（0，1） |