题目内容
6.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=4,那么$\overrightarrow{a}$•(2$\overrightarrow{a}$-$\overrightarrow{b}$)的值为24.分析 由已知求出$\overrightarrow{a}•\overrightarrow{b}$,展开么$\overrightarrow{a}$•(2$\overrightarrow{a}$-$\overrightarrow{b}$),代入数量积得答案.
解答 解:∵向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=4,
∴$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos60°=4×4×\frac{1}{2}=8$,
∴$\overrightarrow{a}$•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=$2|\overrightarrow{a}{|}^{2}-\overrightarrow{a}•\overrightarrow{b}=2×{4}^{2}-8=24$.
故答案为:24.
点评 本题考查平面向量的数量积运算,是基础的计算题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
14.设f(x)=ex(sinx-cosx),其中 0≤x≤2011π,则 f(x)的极大值点个数是( )
| A. | 25 | B. | 1005 | C. | 26 | D. | 28 |
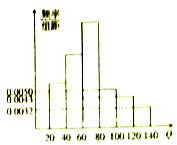 酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.如图为某市交管部门在一次夜间行动中依法查出的60名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中120≤Q<140人数包含Q≥140).
酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.如图为某市交管部门在一次夜间行动中依法查出的60名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中120≤Q<140人数包含Q≥140).