题目内容
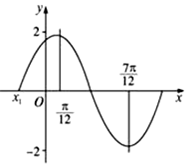
11.设P为函数f(x)=sinπx的图象上的一个最高点,Q为函数g(x)=cosπx的图象上的一个最低点.(1)求|PQ|的最小值;
(2)求f(x)的图象与g(x)的图象的交点中,相邻的三个交点构成的三角形的面积;
(3)求函数f(x)的图象关于直线x=$\frac{1}{4}$对称的函数h(x)图象的解析式,并求出$x∈[-\frac{2}{3},\frac{1}{3}]$的值域.
分析 (1)设出P和Q的坐标,根据两点之间的距离公式求解.
(2)根据正余弦函数的图象可知,相邻的三个交点构成的三角形是一个等腰三角形,其高为$\sqrt{2}$,底边长为一个周期T=2.可求的三角形的面积;
(3)根据函数f(x)的图象关于直线x=$\frac{1}{4}$对称的函数h(x)图象,求出解析式,$x∈[-\frac{2}{3},\frac{1}{3}]$时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的取值最大和最小值,即得到f(x)的值域.
解答 解:(1)P为函数f(x)=sinπx的图象上的一个最高点,Q为函数g(x)=cosπx的图象上的一个最低点.
设f(x)最高点坐标为P$(\frac{1}{2}+2{k_1},1){k_1}∈Z$,g(x)最低点坐标为Q(1+2k2,-1)k2∈Z
∴$|{PQ}|=\sqrt{{{[2{{({k_1}-{k_2})}^2}-\frac{1}{2}]}^2}+4}$
当k1-k2=0时|PQ|min=$\frac{{\sqrt{17}}}{2}$.
(2)函数f(x)=sinπx和函数g(x)=cosπx的周期T=$\frac{2π}{π}=2$,
其相邻的三个交点构成一个等腰三角形,其高为$\sqrt{2}$,底边长为一个周期T=2.
三角形的面积S=$\frac{1}{2}×\sqrt{2}×2$=$\sqrt{2}$;
(3)函数f(x)的图象与函数h(x)图象关于直线x=$\frac{1}{4}$对称,
设h(x)图象上的点M(x,h(x)),关于直线x=$\frac{1}{4}$对称的点N为(x-$\frac{1}{2}$,-h(x)),
N点在函数f(x)的图象上,
∴-h(x)=f(x-$\frac{1}{2}$)=sinπ(x-$\frac{1}{2}$)
∴h(x)=-sin($πx-\frac{π}{2}$)=cosπx
∵$x∈[-\frac{2}{3},\frac{1}{3}]$,
∴πx∈[$-\frac{2π}{3}$,$\frac{π}{3}$]
当$πx=-\frac{2π}{3}$时,函数h(x)取得最小值为$-\frac{1}{2}$,
当πx=0时,函数h(x)取得最大值为1.
故得$x∈[-\frac{2}{3},\frac{1}{3}]$时函数h(x)的值域为 $[-\frac{1}{2},1]$.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,图象对称关系的解析式的求法.属于中档题.

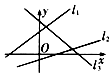
| A. | k1<k2<k3 | B. | k3<k2<k1 | C. | k1<k3<k2 | D. | k2<k1<k3 |
| A. | ${(x-2)^2}+{(y+\frac{3}{2})^2}=\frac{25}{4}$ | B. | ${(x-2)^2}+{(y-\frac{3}{2})^2}=\frac{25}{4}$ | ||
| C. | ${(x+2)^2}+{(y-\frac{3}{2})^2}=\frac{25}{4}$ | D. | ${(x+2)^2}+{(y+\frac{3}{2})^2}=\frac{25}{4}$ |
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.