题目内容
16.已知函数f(x)=lg(mx2+mx+1),若此函数的定义域为R,则实数m的取值范围是[0,4);若此函数的值域为R,则实数m的取值范围是[4,+∞).分析 (1)由题意知mx2+mx+1>0在R上恒成立,因二次项的系数是参数,所以分m=0和m≠0两种情况,再利用二次函数的性质即开口方向和判别式的符号,列出式子求解,最后把这两种结果并在一起;
(2)根据函数的值域为R,则对数的真数式的取值范围包含(0,+∞),由此可得m满足的条件.
解答 解:(1)∵函数f(x)=lg(mx2+mx+1)的定义域为R,
∴mx2+mx+1>0在R上恒成立,
①当m=0时,有1>0在R上恒成立,故符合条件;
②当m≠0时,由$\left\{\begin{array}{l}{m>0}\\{△{=m}^{2}-4m<0}\end{array}\right.$,
解得0<m<4,
综上,实数m的取值范围是[0,4).
(2)令g(x)=mx2+mx+1的值域为A,
∵函数f(x)=lg(mx2+mx+1)的值域为R,
∴(0,+∞)?A,
当m=0时,g(x)=1值域不是为R,不满足条件;
当m≠0时,$\left\{\begin{array}{l}{m>0}\\{{m}^{2}-4m≥0}\end{array}\right.$,解得:m≥4,
故答案为:[0,4),[4,+∞).
点评 本题考查的知识点是对数函数的定义域、值域与最值,二次函数的图象和性质,难度中档.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
7.设a=log23.1,b=logπ2,c=log0.52,则( )
| A. | b>a>c | B. | a>b>c | C. | a>c>b | D. | c>b>a |
8.已知函数f(x)=sinx+cosx,且f'(x)=3f(x),则tanx的值是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
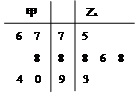 甲乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,
甲乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,