题目内容

14．设f（x）=ex（sinx-cosx），其中 0≤x≤2011π，则 f（x）的极大值点个数是（　　）
A．25B．1005C．26D．28

分析 先求出其导函数，利用导函数得到其单调区间以及其极大值点即可．

解答 解：∵f（x）=ex（sinx-cosx），
∴令f′（x）=ex（sinx-cosx）+ex（cosx+sinx）
=2exsinx=0；
则x=kπ（k∈Z），
故函数f（x）的极大值点为π+2kπ（k∈Z），
即π，3π，5π，7π，…，2009π，共1005个，
故选：B．

点评 本题考查了导数的应用以及函数的极值问题，考查三角函数问题，是一道中档题．

练习册系列答案
相关题目
4．设正项等比数列{an}的前n项和为Sn，且满足S3=3a3+2a2，a4=8．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列bn=log2an，求{|bn|}的前n项和Tn．
5．若不等式$\frac{ax-1}{x+1}$＜1的解集是（-1，1），则a=3．
2．如图，已知直线l1，l2，l3的斜率分别为k1，k2，k3，则（　　）
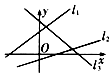
A．k1＜k2＜k3B．k3＜k2＜k1C．k1＜k3＜k2D．k2＜k1＜k3
9．计算log25•log32•log53的值为（　　）
A．1B．2C．4D．8
19．求函数y=sin（2x-$\frac{π}{3}$）的单调递减区间，并叙述怎样由函数y=sinx的图象变换得到函数y=sin（2x-$\frac{π}{3}$）的图象．
6．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=4，那么$\overrightarrow{a}$•（2$\overrightarrow{a}$-$\overrightarrow{b}$）的值为24．
3．
商店名称ABCDE
销售额x（千万元）35679
利润额y（百万元）23345
（1）画出散点图．观察散点图，说明两个变量有怎样的相关性．
（2）用最小二乘法计算利润额y对销售额x的回归直线方程．
（3）当销售额为4（千万元）时，估计利润额的大小．
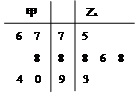4．甲乙两位歌手在“中国好声音”选拔赛中，5次得分情况如茎叶图所示，
（1）求甲乙两位歌手这5次得分的平均分
（2）请分析甲乙两位歌手这5次得分中谁的成绩更稳定．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网