题目内容
15.将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,用y表示点数之和.(1)求事件“y=4”的概率;
(2)求事件“y≤10”的概率.
分析 (1)先求出基本数值总数n=6×6=36,再用列举法求出事件“y=4”包含的基本事件个数,由此能出事件“y=4”的概率.
(2)利用列举法求出事件“y≤10”包含的基本事件个数,由此能出事件“y≤10”的概率.
解答 解:(1)将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,
用y表示点数之和.
则基本数值总数n=6×6=36,
事件“y=4”包含的基本事件有:
(1,3),(3,1),(2,2),共3个,
∴事件“y=4”的概率p=$\frac{3}{36}=\frac{1}{12}$.
(2)事件“y≤10”包含的基本事件有:
(1,1),(1,2),(2,1),(1,3),(3,1),(1,4),(4,1),(1,5),(5,1),(1,6),(6,1),
(2,2),(2,3),(3,2),(2,4),(4,2),(2,5),(5,2),(2,6),(6,2),(3,3),(3,4),
(4,3),(3,5),(5,3),(3,6),(6,3),(4,4),(4,5),(5,4),(4,6),(6,4),(5,5),
共有33个,
∴事件“y≤10”的概率p=$\frac{33}{36}=\frac{11}{12}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
3.
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.

| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.

10.用数字1,2,3,4,5组成的无重复数字的四位偶数的个数为( )
| A. | 120 | B. | 240 | C. | 24 | D. | 48 |
7.设a=log23.1,b=logπ2,c=log0.52,则( )
| A. | b>a>c | B. | a>b>c | C. | a>c>b | D. | c>b>a |
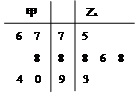 甲乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,
甲乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,