题目内容
下面命题正确的序号是
①一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为
=7.19x+73.93,用这个模型预测这个孩子10岁时的身高,则身高一定是145.83cm
②设有一个回归方程为
=2-1.5则变量x增加一个单位时,y平均减少1.5个单位③结构图反应事物的逻辑关系而不是流程图中的先后顺序关系.
④若x∈(-∞,1),则函数y=
有最小值1
⑤对一切满足|x|+|y|≤1的实数x,y,不等式|2x-3y+
|+|y-1|+|2y-x-3|≤a恒成立,则实数a的最小值为
.
①一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为
 |
| y |
②设有一个回归方程为
 |
| y |
④若x∈(-∞,1),则函数y=
| x2-2x+2 |
| 2x-2 |
⑤对一切满足|x|+|y|≤1的实数x,y,不等式|2x-3y+
| 3 |
| 2 |
| 23 |
| 2 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:通过对回归直线方程的理解可判断①和②的真假;由结构图的定义判断③;配方后利用基本不等式求最值判断④;数形结合利用线性规划知识解决⑤.
解答:
解:对于①,当x=10时,
=7.19×10+73.93=145.83,
∵回归直线是用来估计总体的,
∴我们求的值都是估算值,得到的结果也是近似的,孩子的身高近似为145.83cm,不一定就是145.83cm,∴①错误;
对于②,对方程
=2-1.5x来说,当自变量x增加一个单位,变为x+1时,
=2-1.5(x+1),
即
=2-1.5x-1.5=0.5-1.5x,
∴当变量x增加一个单位时,y平均减少1.5个单位.
∴②正确;
对于③,结构图反应事物的逻辑关系而不是流程图中的先后顺序关系.
∴③正确;
对于④,y=
=
=
[(x-1)+
],
当x<1时,y=-
[(1-x)+
]≤-
×2
=-1.
∴若x∈(-∞,1),则函数y=
有最大值-1.
命题④错误;
对于⑤,∵|x|+|y|≤1,所表示的平面区域如图,
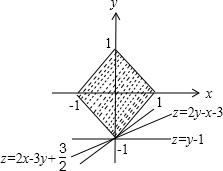
由图可知,当实数x,y为可行域内点(0,-1)的横纵坐标时,
2x-3y+
有正的最大值,y-1,2y-x-3均为负的最小值.
此时|2x-3y+
|+|y-1|+|2y-x-3|有最大值为
.
∴使不等式|2x-3y+
|+|y-1|+|2y-x-3|≤a恒成立的实数a的最小值为
.
命题⑤正确.
故答案为:②③⑤.
 |
| y |
∵回归直线是用来估计总体的,
∴我们求的值都是估算值,得到的结果也是近似的,孩子的身高近似为145.83cm,不一定就是145.83cm,∴①错误;
对于②,对方程
 |
| y |
 |
| y |
即
 |
| y |
∴当变量x增加一个单位时,y平均减少1.5个单位.
∴②正确;
对于③,结构图反应事物的逻辑关系而不是流程图中的先后顺序关系.
∴③正确;
对于④,y=
| x2-2x+2 |
| 2x-2 |
| (x-1)2+1 |
| 2(x-1) |
| 1 |
| 2 |
| 1 |
| x-1 |
当x<1时,y=-
| 1 |
| 2 |
| 1 |
| 1-x |
| 1 |
| 2 |
(1-x)•
|
∴若x∈(-∞,1),则函数y=
| x2-2x+2 |
| 2x-2 |
命题④错误;
对于⑤,∵|x|+|y|≤1,所表示的平面区域如图,

由图可知,当实数x,y为可行域内点(0,-1)的横纵坐标时,
2x-3y+
| 3 |
| 2 |
此时|2x-3y+
| 3 |
| 2 |
| 23 |
| 2 |
∴使不等式|2x-3y+
| 3 |
| 2 |
| 23 |
| 2 |
命题⑤正确.
故答案为:②③⑤.
点评:本题考查命题的真假判断与应用,考查了数形结合的解题思想方法,正确解答⑤是解决该题的关键,是中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
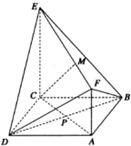 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,CE=2AF=2
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,CE=2AF=2