题目内容
已知函数f（x）=cosx，f′（x）是它的导函数，则f′（
）= ．
| π |
| 3 |
考点：导数的运算
专题：导数的综合应用
分析：由求导公式求出函数的导数，再代入自变量的值即可计算出结果
解答：
解：由f（x）=cosx，得f′（x）=-sinx-
∴则f′（
）=-sin
=-
故答案为：-
| ||
| 2 |
∴则f′（
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
故答案为：-
| ||
| 2 |
点评：本题考查利用导数公式计算，属于基本计算题，熟练掌握公式是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
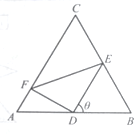如图，正三角形ABC的边长为2，D、E、F分别在三边AB，BC和CA上，且D为AB的中点，∠EDF=90°，∠BDE=θ（0°＜θ＜90°）．
