题目内容
二次曲线
,(t为参数)的左焦点的坐标是 ,若P为曲线上对应t=
的点,则直线OP的斜率是 ,|OP|= .
|
| π |
| 6 |
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:利用参数方程化为直角坐标方程,然后求出焦点坐标,利用曲线上点的坐标求出直线的斜率,得到距离.
解答:
解:二次曲线
,(t为参数)的普通方程为:
+
=1,
a=3,b=2,∴c=
.左焦点的坐标是(-
,0).
P为曲线上对应t=
的点,P(
,1).直线的斜率为:
=
.
|PO|=
=
.
故答案为:(-
,0);
;
.
|
| x2 |
| 9 |
| x2 |
| 4 |
a=3,b=2,∴c=
| 5 |
| 5 |
P为曲线上对应t=
| π |
| 6 |
3
| ||
| 2 |
| 1 | ||||
|
2
| ||
| 9 |
|PO|=
(
|
| ||
| 2 |
故答案为:(-
| 5 |
2
| ||
| 9 |
| ||
| 2 |
点评:本题考查曲线参数方程与普通方程的转化,椭圆的基本性质,直线的斜率的分,考查计算能力.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
“x=1”是“x2-1=0”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、既非充分也非必要条件 |
| D、充分不必要条件 |
不等式x2-3x+2>0的解集为( )
| A、(-∞,-2)∪(-1,+∞) |
| B、(-∞,1)∪(2,+∞) |
| C、(-2,-1) |
| D、(1,2) |
 如图,有一菱形纸片ABCD,∠A=60°,E是AD边上的一点(不包括A,D),先将ABCD沿对角线BD折成直二面角,再将△ABE沿BE翻折到△A′BE,下列不可能正确的是( )
如图,有一菱形纸片ABCD,∠A=60°,E是AD边上的一点(不包括A,D),先将ABCD沿对角线BD折成直二面角,再将△ABE沿BE翻折到△A′BE,下列不可能正确的是( )| A、BC与平面A′BE内某直线平行 |
| B、BC与平面A′BE内某直线垂直 |
| C、CD∥平面A′BE |
| D、CD⊥平面A′BE |
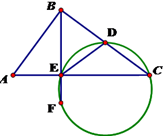 如图,在△ABC中,AB=3,BC=4,CA=5,D是BC的中点,BE⊥AC于E,BE的延长线交△DEC的外接圆于F,则EF的长为
如图,在△ABC中,AB=3,BC=4,CA=5,D是BC的中点,BE⊥AC于E,BE的延长线交△DEC的外接圆于F,则EF的长为