题目内容
函数f(x)=max{x2-x,1-x2}的单调增区间是( )
A、[-
| ||
B、(-∞,-
| ||
C、[-
| ||
| D、[0,1] |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:作出两个函数的图象,利用数形结合即可得到结论.
解答:
 解:由x2-x=1-x2得2x2-x-1=0,
解:由x2-x=1-x2得2x2-x-1=0,
解得x=1或x=-
,
当x≥1或x≤-
,f(x)=max{x2-x,1-x2}=x2-x,此时函数的递增区域为[1,+∞),
当-
<x<1,f(x)=max{x2-x,1-x2}=1-x2,此时函数的递增区域为[-
,0],
综上函数的递增区间为[-
,0],[1,+∞),
故选:A
 解:由x2-x=1-x2得2x2-x-1=0,
解:由x2-x=1-x2得2x2-x-1=0,解得x=1或x=-
| 1 |
| 2 |
当x≥1或x≤-
| 1 |
| 2 |
当-
| 1 |
| 2 |
| 1 |
| 2 |
综上函数的递增区间为[-
| 1 |
| 2 |
故选:A
点评:本题主要考查函数单调性和单调区间的求解,求出函数f(x)的表达式是解决本题的关键.

练习册系列答案
相关题目
关于x的不等式2ax2+ax-
<0对一切实数x都成立,则a的取值范围是( )
| 3 |
| 8 |
| A、(-3,0) |
| B、(0,3) |
| C、[-3,0) |
| D、(-3,0] |
已知变量x,y满足约束条件
,则z=2x+y的最小值为( )
|
| A、0 | B、1 | C、4 | D、6 |
在等差数列{an}中,已知a2+a10=16,则a4+a8=( )
| A、12 | B、16 | C、20 | D、24 |
 如图,M,N分别是四面体OABC的边OA,BC的中点,E是MN的三等分点,且
如图,M,N分别是四面体OABC的边OA,BC的中点,E是MN的三等分点,且| NE |
| NM |
| 1 |
| 3 |
| OA |
| OB |
| OC |
| OE |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
圆锥的底面半径为1,侧面展开图是一个半圆,则此圆锥的表面积为( )
| A、6π | ||||
| B、5π | ||||
| C、3π | ||||
D、
|
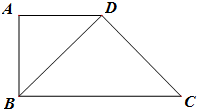 如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题:
如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题: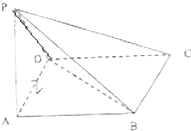 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=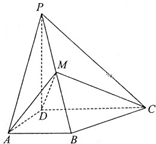 如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=2,PD=
如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=2,PD=