题目内容
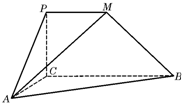 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.(Ⅰ)求二面角M-AC-B的余弦值;
(Ⅱ)求点C到面MAB的距离.
考点:用空间向量求平面间的夹角,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(Ⅰ)建立空间直角坐标系C-xyz,利用向量法能求出二面角M-AC-B的余弦值.
(Ⅱ)求出平面MAB的一个法向量,利用向量法能求出点C到平面MAB的距离.
(Ⅱ)求出平面MAB的一个法向量,利用向量法能求出点C到平面MAB的距离.
解答:
解: (Ⅰ)∵PC⊥AB,PC⊥BC,AB∩BC=B,∴PC⊥平面ABC.
(Ⅰ)∵PC⊥AB,PC⊥BC,AB∩BC=B,∴PC⊥平面ABC.
在平面ABC内,过C作CD⊥CB,
建立空间直角坐标系C-xyz(如图)
由题意有A(
,-
,0),设P(0,0,z0)(z0>0),
则M(0,1,z0),
=(
,-
,z0),
=(0,0,z0)
由直线AM与直线PC所成的角为600,
得
•
=|
|•|
|•cos600,
即z02=
•z0,解得z0=1
∴
=(0,0,1),
=(
,-
,0),
设平面MAC的一个法向量为
=(x1,y1,z1),
则
,取x1=1,得
=(1,
,-
),
平面ABC的法向量取为
=(0,0,1)
设
与
所成的角为θ,则cosθ=
=
.
二面角M-AC-B的平面角为锐角,
故二面角M-AC-B的余弦值为
.…(5分)
(Ⅱ)M(0,1,1),A(-
,-
,0),B(0,2,0),
∴
=(
,
,1),
=(0,1,-1).
设平面MAB的一个法向量
=(x2,y2,z2),
则
,
取z2=1,得
=(
,-1,-1),
则点C到平面MAB的距离d=
=
.…(10分)
 (Ⅰ)∵PC⊥AB,PC⊥BC,AB∩BC=B,∴PC⊥平面ABC.
(Ⅰ)∵PC⊥AB,PC⊥BC,AB∩BC=B,∴PC⊥平面ABC.在平面ABC内,过C作CD⊥CB,
建立空间直角坐标系C-xyz(如图)
由题意有A(
| ||
| 2 |
| 1 |
| 2 |
则M(0,1,z0),
| AM |
| ||
| 2 |
| 1 |
| 2 |
| CP |
由直线AM与直线PC所成的角为600,
得
| AM |
| CP |
| AM |
| CP |
即z02=
| π |
| 2 |
| z02+3 |
∴
| CM |
| CA |
| ||
| 2 |
| 1 |
| 2 |
设平面MAC的一个法向量为
| n1 |
则
|
| n1 |
| 3 |
| 3 |
平面ABC的法向量取为
| n2 |
设
| n1 |
| n2 |
| ||||
|
|
-
| ||
|
二面角M-AC-B的平面角为锐角,
故二面角M-AC-B的余弦值为
| ||
| 7 |
(Ⅱ)M(0,1,1),A(-
| ||
| 2 |
| 1 |
| 2 |
∴
| AM |
| ||
| 2 |
| 3 |
| 2 |
| MB |
设平面MAB的一个法向量
| m |
则
|
取z2=1,得
| m |
| 5 | ||
|
则点C到平面MAB的距离d=
|
| ||||
|
|
2
| ||
| 31 |
点评:本题考查二面角的求法,考查点到平面的距离的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
已知数列{an}是等差数列,若a1+a5=24,a4=8,则数列{an}的公差等于( )
| A、6 | B、-6 | C、4 | D、-4 |
在等差数列{an}中,已知a2+a10=16,则a4+a8=( )
| A、12 | B、16 | C、20 | D、24 |
 如图,M,N分别是四面体OABC的边OA,BC的中点,E是MN的三等分点,且
如图,M,N分别是四面体OABC的边OA,BC的中点,E是MN的三等分点,且| NE |
| NM |
| 1 |
| 3 |
| OA |
| OB |
| OC |
| OE |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
圆锥的底面半径为1,侧面展开图是一个半圆,则此圆锥的表面积为( )
| A、6π | ||||
| B、5π | ||||
| C、3π | ||||
D、
|
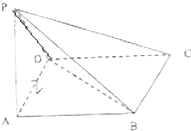 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=