题目内容
过点(
,
)且被圆C:x2+y2-2x-4y=0截得的最短弦的弦长为( )
| 5 |
| 2 |
| 3 |
| 2 |
A、3
| ||
B、
| ||
C、
| ||
D、
|
考点:直线与圆相交的性质
专题:直线与圆
分析:根据点A(
,
)满足AC小于半径,可得点A在圆C的内部,故当AC和弦垂直时,弦长最短.再利用弦长公式求得最短弦长.
| 5 |
| 2 |
| 3 |
| 2 |
解答:
解:圆C:x2+y2-2x-4y=0,即 (x-1)2+(y-2)2=5,表示以C(1,2)为圆心,半径等于
的圆,
由于点A(
,
)满足AC=
<
,可得点A在圆C的内部,
故当AC和弦垂直时,弦长最短.
此时,弦长为2
=2
=
,
故选:B.
| 5 |
由于点A(
| 5 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 5 |
故当AC和弦垂直时,弦长最短.
此时,弦长为2
| r2-AC2 |
5-
|
| 10 |
故选:B.
点评:本题主要考查直线和圆相交的性质,弦长公式的应用,属于基础题.

练习册系列答案
相关题目
关于x的不等式2ax2+ax-
<0对一切实数x都成立,则a的取值范围是( )
| 3 |
| 8 |
| A、(-3,0) |
| B、(0,3) |
| C、[-3,0) |
| D、(-3,0] |
已知数列{an}是等差数列,若a1+a5=24,a4=8,则数列{an}的公差等于( )
| A、6 | B、-6 | C、4 | D、-4 |
函数f(x)=lg|x|-sinx的零点个数为( )
| A、8 | B、6 | C、5 | D、3 |
甲、乙同时炮击一架敌机,已知甲击中敌机的概率为0.3,乙击中敌机的概率为0.5,敌机被击中的概率为( )
| A、0.95 | B、0.8 |
| C、0.65 | D、0.15 |
已知变量x,y满足约束条件
,则z=2x+y的最小值为( )
|
| A、0 | B、1 | C、4 | D、6 |
在等差数列{an}中,已知a2+a10=16,则a4+a8=( )
| A、12 | B、16 | C、20 | D、24 |
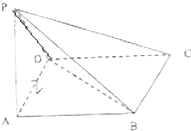 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=