题目内容
已知向量
=(3,4),
=(x,1)且(
+
)•
=|
|,则实数x的值为 .
| a |
| b |
| a |
| b |
| b |
| a |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:运用向量的数量积的坐标表示和向量模的公式,及向量的平方即为模的平方,解方程即可得到.
解答:
解:向量
=(3,4),
=(x,1)
则
•
=3x+4,|
|=5,|
|=
,
由(
+
)•
=|
|,
可得
•
+
2=|
|,
即3x+4+1+x2=5,
解得x=0或-3,
故答案为:0或-3.
| a |
| b |
则
| a |
| b |
| a |
| b |
| 1+x2 |
由(
| a |
| b |
| b |
| a |
可得
| a |
| b |
| b |
| a |
即3x+4+1+x2=5,
解得x=0或-3,
故答案为:0或-3.
点评:本题考查向量的数量积的坐标表示和向量的模的公式,考查运算能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=log
(4-x2)的单调递减区间是( )
| 1 |
| 3 |
| A、(-2,0) |
| B、(0,2) |
| C、(-∞,-2) |
| D、(2,+∞) |
函数y=log
(x2-3x+2)的单调递增区间为( )
| 1 |
| 2 |
| A、(-∞,1) | ||
B、(-∞,
| ||
C、[
| ||
| D、(2,+∞) |
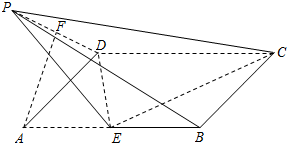 如图所示,在矩形ABCD中,AD=1,AB=2,点E是线段AB的中点,把三角形AED沿DE折起,设折起后点A的位置为 P,F是PD的中点.
如图所示,在矩形ABCD中,AD=1,AB=2,点E是线段AB的中点,把三角形AED沿DE折起,设折起后点A的位置为 P,F是PD的中点.