题目内容
已知集合A={a1,a2,a3,..,an,}其中ai∈R(1≤i≤n,n>2),f(A)表示和ai+aj(1≤i<j≤n)中所有不同值的个数.若集合A={2,4,8,…,2n}.
(1)当n=4时,f(A)= ;
(2)当n∈N*且n≥2时,归纳出f(A)关于n的解析式为 .
(1)当n=4时,f(A)=
(2)当n∈N*且n≥2时,归纳出f(A)关于n的解析式为
考点:归纳推理
专题:计算题,推理和证明
分析:(1)根据定义结合题中所给的集合即可确定当n=4时的f(A);
(2)根据集合A的元素特点,归纳出f(A)关于n的解析式.
(2)根据集合A的元素特点,归纳出f(A)关于n的解析式.
解答:
解:(1)由2+4=6,2+8=10,2+16=18,4+8=12,4+16=20,8+16=24,
得当n=4时,f(A)=6.
(2)集合A={2,4,8,…,2n}.
利用组合知识可得f(A)=
=
.
故答案为:6;f(A)=
.
得当n=4时,f(A)=6.
(2)集合A={2,4,8,…,2n}.
利用组合知识可得f(A)=
| C | 2 n |
| n(n-1) |
| 2 |
故答案为:6;f(A)=
| n(n-1) |
| 2 |
点评:本题主要考查集合与元素的关系,以及组合的有关知识,认真审题,正确的理解题意并且仔细解答是解题的关键点

练习册系列答案
相关题目
设函数f(x)的定义域为R,且对任意的实数x,满足f(2-x)=f(2+x),f(5-x)=f(5+x),且f(0)=0,则f(x)在区间[-18,18]上至少有个( )零点.
| A、10 | B、11 | C、12 | D、13 |
已知函数f(x)=x2+2bx的图象在点A(0,f(0))处的切线l与直线x-y+3=0平行,若数列{
}的前n项和为S2015的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
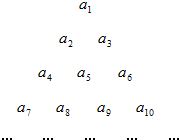 已知数列{an}中,a1=2,a5=10,an+2=2an+1-an(n∈N*),把数列{an}的各项排成如图所示的三角形状,记F(m,n)表示第m行、第n列的项,若F(m,n)+F(m+1,n+1)=90,则m+n=
已知数列{an}中,a1=2,a5=10,an+2=2an+1-an(n∈N*),把数列{an}的各项排成如图所示的三角形状,记F(m,n)表示第m行、第n列的项,若F(m,n)+F(m+1,n+1)=90,则m+n=