题目内容
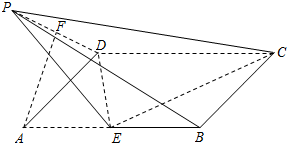 如图所示,在矩形ABCD中,AD=1,AB=2,点E是线段AB的中点,把三角形AED沿DE折起,设折起后点A的位置为 P,F是PD的中点.
如图所示,在矩形ABCD中,AD=1,AB=2,点E是线段AB的中点,把三角形AED沿DE折起,设折起后点A的位置为 P,F是PD的中点.(1)求证:无论P在什么位置,都有 AF∥平面 PEC;(2)当点P在平面ABCD上的射影落在线段DE上时,若三棱锥P-ECD的四个顶点都在一个球上,求这个球的体积.
考点:直线与平面平行的判定,球的体积和表面积
专题:空间位置关系与距离
分析:(1)根据面面平行得到线面平行;(2)画出图象,求出外接球的半径,从而求出球的体积.
解答:
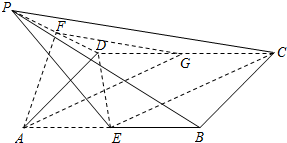 (1)证明:设CD的中点是G,连接AG、FG,
(1)证明:设CD的中点是G,连接AG、FG,
∵CG∥AE,CG=AE,
∴四边形AECG是平行四边形,
∴AG∥EC,
∵AG?平面PEC,EC?平面PEC,
∴AG∥平面PEC,
又∵FG∥PC,FG?平面PEC,PC?平面PEC,
∴FG∥平面PEC,
∵FG?平面AGF,AG?平面AGF,FG∩AG=G,
∴平面AGF∥平面PEC,而AF?平面AGF,
∴AF∥平面PEC;
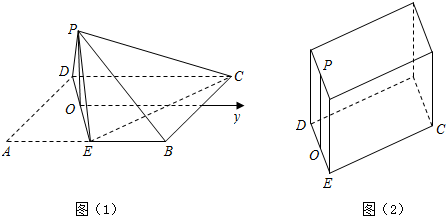
(2)解:如图(1)所示,
∵PD=PE=1,若点P的射影为O,
∵点P的射影在线段DE上,
∴O是线段DE的中点,且PO⊥平面EBCO,
∵△PDE是等腰直角三角形,PD=PE=1,
∴OP=
,
由△ECD是等腰直角三角形,∠DEC=90°,
∴三棱锥P-ECD的外接球是如图(2)所示的长方体的外接球,
∴外接球的半径R=
=
,
∴V=
πR3=
.
 (1)证明:设CD的中点是G,连接AG、FG,
(1)证明:设CD的中点是G,连接AG、FG,∵CG∥AE,CG=AE,
∴四边形AECG是平行四边形,
∴AG∥EC,
∵AG?平面PEC,EC?平面PEC,
∴AG∥平面PEC,
又∵FG∥PC,FG?平面PEC,PC?平面PEC,
∴FG∥平面PEC,
∵FG?平面AGF,AG?平面AGF,FG∩AG=G,
∴平面AGF∥平面PEC,而AF?平面AGF,
∴AF∥平面PEC;
(2)解:如图(1)所示,
∵PD=PE=1,若点P的射影为O,
∵点P的射影在线段DE上,
∴O是线段DE的中点,且PO⊥平面EBCO,
∵△PDE是等腰直角三角形,PD=PE=1,
∴OP=
| ||
| 2 |
由△ECD是等腰直角三角形,∠DEC=90°,
∴三棱锥P-ECD的外接球是如图(2)所示的长方体的外接球,
∴外接球的半径R=
| 1 |
| 2 |
|
3
| ||
| 4 |
∴V=
| 4 |
| 3 |
9
| ||
| 8 |

点评:本题考查了线面,面面的平行的性质以及判断,考查了球的体积问题,本题属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)的定义域为R,且对任意的实数x,满足f(2-x)=f(2+x),f(5-x)=f(5+x),且f(0)=0,则f(x)在区间[-18,18]上至少有个( )零点.
| A、10 | B、11 | C、12 | D、13 |
点M(1,1)到抛物线y=ax2准线的距离为2,则a的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知函数f(x)=x2+2bx的图象在点A(0,f(0))处的切线l与直线x-y+3=0平行,若数列{
}的前n项和为S2015的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
 有一个所有棱长均为a的正四棱锥P-ABCD,还有一个所有棱长均为a的正三棱锥.将此三棱锥的一个面与正四棱锥的一个侧面完全重合地粘在一起,得到一个如图所示的多面体.
有一个所有棱长均为a的正四棱锥P-ABCD,还有一个所有棱长均为a的正三棱锥.将此三棱锥的一个面与正四棱锥的一个侧面完全重合地粘在一起,得到一个如图所示的多面体.