题目内容
直线l1:y=kx+1与圆心C:x2+y2+kx-y-4=0的两个交点关于直线l2:x+y=0对称,则这样的两个点的坐标是 .
考点:直线与圆的位置关系
专题:直线与圆
分析:利用垂直关系求出k,得到直线方程与圆的方程,联立求出交点坐标即可.
解答:
解:直线l1:y=kx+1与圆心C:x2+y2+kx-y-4=0的两个交点关于直线l2:x+y=0对称,
所以k=1,
直线l1:y=x+1与圆心C:x2+y2+x-y-4=0联立消去y可得:x2+x-2=0,
解得x=1或x=-2.
x=1时,y=2,x=-2时,y=-1.
所求的两个点的坐标是(1,2)或(-2,-1).
故答案为:(1,2)或(-2,-1).
所以k=1,
直线l1:y=x+1与圆心C:x2+y2+x-y-4=0联立消去y可得:x2+x-2=0,
解得x=1或x=-2.
x=1时,y=2,x=-2时,y=-1.
所求的两个点的坐标是(1,2)或(-2,-1).
故答案为:(1,2)或(-2,-1).
点评:本题考查直线与圆的位置关系的应用,对称知识的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
若a=
xdx,b=
dx,c=
2dx,则a,b,c的大小关系为( )
| ∫ | 4 2 |
| ∫ | 4 2 |
| 4 |
| x |
| ∫ | 4 2 |
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、c<b<a |
在数38,47,56,65中,最大的一个是( )
| A、38 |
| B、47 |
| C、56 |
| D、65 |
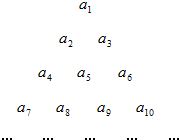 已知数列{an}中,a1=2,a5=10,an+2=2an+1-an(n∈N*),把数列{an}的各项排成如图所示的三角形状,记F(m,n)表示第m行、第n列的项,若F(m,n)+F(m+1,n+1)=90,则m+n=
已知数列{an}中,a1=2,a5=10,an+2=2an+1-an(n∈N*),把数列{an}的各项排成如图所示的三角形状,记F(m,n)表示第m行、第n列的项,若F(m,n)+F(m+1,n+1)=90,则m+n=