题目内容
两个人射击,甲射击一次中靶概率是p1,乙射击一次中靶概率是p2,已知,p1,p2是方程 3x2-x=0的根,若两人各射击5次,甲的方差是
.
(Ⅰ)求 p1,p2的值;
(Ⅱ)两人各射击2次,中靶至少3次就算完成目的,则完成目的概率是多少?
(Ⅲ)甲、乙两人轮流射击,各射击3次,中靶一次就终止射击,求终止射击时两人射击的次数之和ξ的期望?
| 5 |
| 4 |
(Ⅰ)求 p1,p2的值;
(Ⅱ)两人各射击2次,中靶至少3次就算完成目的,则完成目的概率是多少?
(Ⅲ)甲、乙两人轮流射击,各射击3次,中靶一次就终止射击,求终止射击时两人射击的次数之和ξ的期望?
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(Ⅰ)由题意可知 ξ甲~B(5,p1),由此能求出p1,p2的值.
(Ⅱ)共击中3次概率C22(
)2(1-
)0×C21(
)1(
)1+C21(
)1(
)1×C22(
)2(
)0=
;共击中4次概率C22(
)2(
)0×C22(
)2(
)0=
. 由此能求出完成目的概率.
(Ⅲ) 由已恬ξ=1,2,3,4,5,6,分别求出相应的概率,由此能求出终止射击时两人射击的次数之和ξ的期望.
(Ⅱ)共击中3次概率C22(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 36 |
(Ⅲ) 由已恬ξ=1,2,3,4,5,6,分别求出相应的概率,由此能求出终止射击时两人射击的次数之和ξ的期望.
解答:
解:(Ⅰ)由题意可知 ξ甲~B(5,p1),
∴Dξ甲=5p1 (1-p1)=
,p12-p1+
=0,解得p1=
;
又
,
是方程 x2-5x+6=0的根,
∴
•
=6,∴p2=
.
(Ⅱ)两类情况:
∴共击中3次概率C22(
)2(1-
)0×C21(
)1(
)1+C21(
)1(
)1×C22(
)2(
)0=
;
共击中4次概率C22(
)2(
)0×C22(
)2(
)0=
.
∴所求概率为
+
=
.
(Ⅲ) P(ξ=1)=
,P(ξ=2)=(1-
)×
=
,
P(ξ=3)=(1-
)×
×
=
,
P(ξ=4)=(1-
)2×
×
=
,
P(ξ=5)=(1-
)2×(
)2×
=
,
P(ξ=6)=(1-
)3×(
)2×1=
,
ξ的分布列为:
Eξ=1×
+(2+3)×
+(4+5+6)×
=
.
∴Dξ甲=5p1 (1-p1)=
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
又
| 1 |
| p1 |
| 1 |
| p2 |
∴
| 1 |
| p1 |
| 1 |
| p2 |
| 1 |
| 3 |
(Ⅱ)两类情况:
∴共击中3次概率C22(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
共击中4次概率C22(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 36 |
∴所求概率为
| 1 |
| 6 |
| 1 |
| 36 |
| 7 |
| 36 |
(Ⅲ) P(ξ=1)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
P(ξ=3)=(1-
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
P(ξ=4)=(1-
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 18 |
P(ξ=5)=(1-
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 18 |
P(ξ=6)=(1-
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 18 |
ξ的分布列为:
| P | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||||
| ξ |
|
|
|
|
|
|
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 18 |
| 13 |
| 6 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
设集合A={x|1<x≤2},B={ x|x<a},若A⊆B,则a的取值范围是( )
| A、{a|a≥1} |
| B、{a|a≤1} |
| C、{a|a≥2} |
| D、{a|a>2} |
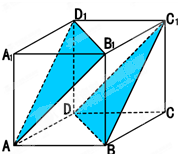 已知正方体ABCD-A1B1C1D1.求证:
已知正方体ABCD-A1B1C1D1.求证: