题目内容
已知函数f(x)=lnx,g(x)=x+a.
(1)当a=0时,求函数y=f(x)•g(x)的单调区间;
(2)当a∈R且|a|≥1时,讨论函数F(x)=
的极值点个数.
(1)当a=0时,求函数y=f(x)•g(x)的单调区间;
(2)当a∈R且|a|≥1时,讨论函数F(x)=
| f[g(x)] |
| f(x) |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:(1)当a=0时,y=f(x)•g(x)=xlnx的定义域为(0,+∞),求导y'=lnx+x
=lnx+1,由导数的正负确定函数的单调区间;
(2)化简F(x)=
=
(x>0且x≠1),求导并令导数为0,化为函数y=xlnx有相同的函数值时,自变量分别为x+a,x;由(1)可得|a|<1,故不成立,故当|a|≥1时,函数F(x)无极值点.
| 1 |
| x |
(2)化简F(x)=
| f[g(x)] |
| f(x) |
| ln(x+a) |
| lnx |
解答:
解:(1)当a=0时,y=f(x)•g(x)=xlnx的定义域为(0,+∞),
y'=lnx+x
=lnx+1,又∵当x=
时,y'=0,
则函数y=f(x)•g(x)在(0,
)上单调递减,在(
,+∞)上单调递增;
(2)F(x)=
=
(x>0且x≠1),
则令F'(x)=
=0,
即
ln(x+a)-
lnx=0,
即(x+a)ln(x+a)-xlnx=0,
若方程有解,
可化为函数y=xlnx有相同的函数值时,自变量分别为x+a,x;
由(1)知,y=xlnx在(0,
)上单调递减,在(
,+∞)上单调递增;
故在(0,
)上,y<0,在(
,1)上,y<0,在(1,+∞)上,y>0,
故|x+a-x|=|a|<1,
则方程也解,即不存在x,使F'(x)=0成立;
即,当|a|≥1时,函数F(x)无极值点.
y'=lnx+x
| 1 |
| x |
| 1 |
| e |
则函数y=f(x)•g(x)在(0,
| 1 |
| e |
| 1 |
| e |
(2)F(x)=
| f[g(x)] |
| f(x) |
| ln(x+a) |
| lnx |
则令F'(x)=
| ||||
| (lnx)2 |
即
| 1 |
| x |
| 1 |
| x+a |
即(x+a)ln(x+a)-xlnx=0,
若方程有解,
可化为函数y=xlnx有相同的函数值时,自变量分别为x+a,x;
由(1)知,y=xlnx在(0,
| 1 |
| e |
| 1 |
| e |
故在(0,
| 1 |
| e |
| 1 |
| e |
故|x+a-x|=|a|<1,
则方程也解,即不存在x,使F'(x)=0成立;
即,当|a|≥1时,函数F(x)无极值点.
点评:本题考查了导数的综合应用,导数的正负可判断函数的单调性,可导时,存在零点的必要条件是导数为0;从而判断零点的个数,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“sinθ•cosθ>0”是“θ是第一象限角”的( )
| A、充分必要条件 |
| B、充分非必要条件 |
| C、必要非充分条件 |
| D、非充分非必要条件 |
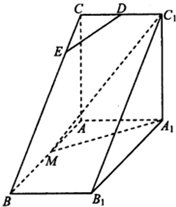 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点. 若f(x)=sin(
若f(x)=sin(