化简sin2α+sin2β-sin2αcos2β-sin2αsin2β的结果为．题目和参考答案——青夏教育精英家教网—

题目内容

化简sin²α+sin²β-sin²αcos²β-sin²αsin²β的结果为

．

考点：三角函数的化简求值,同角三角函数基本关系的运用

专题：计算题,三角函数的求值

分析：先对原式进行合并同类项，利用同角三角函数基本关系，进行化简求值．

解答： 解：sin²α+sin²β-sin²αcos²β-sin²αsin²β
=sin²α（1-cos²β）+sin²β（1-sin²α）
=sin²αsin²β+sin²βcos²α
=sin²β（sin²α+cos²α）
=sin²β
故答案为；sin²β

点评：本题主要考查了同角三角函数的基本关系对函数进行化简求值．

练习册系列答案

金榜题名系列丛书新课标快乐假期寒系列答案

相关题目

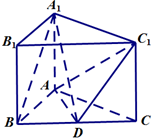如图三棱柱ABC-A₁B₁C₁中，侧棱与底面垂直，△ABC是等边三角形，点D是BC的中点．
（Ⅰ）证明：A₁B∥平面C₁AD；
（Ⅱ）若在三棱柱ABC-A₁B₁C₁内部（含表面）随机投放一个点P，求点P落在三棱锥C₁-A₁AD内部（含表面）的概率．

在一次数学测验后，班级学委王明对选答题的选题情况进行了统计，如下表：（单位：人）

	几何证明选讲	坐标系与参数方程	不等式选讲	合计
男同学	12	4	6	22
女同学	0	8	12	20
合计	12	12	18	42

（Ⅰ）在统计结果中，如果把《几何证明选讲》和《坐标系与参数方程》称为几何类，把《不等式选讲》称为代数类，我们可以得到如下2×2列联表：（单位：人）

	几何类	代数类	总计
男同学	16	6	22
女同学	8	12	20
总计	24	18	42

据此判断是否有95%的把握认为选做“几何类”或“代数类”与性别有关？
（Ⅱ）在原统计结果中，如果不考虑性别因素，按分层抽样的方法从选做不同选做题的同学中随机选出7名同学进行座谈．已知学委王明和两名数学科代表三人都在选做《不等式选讲》的同学中．
①求在这名班级学委被选中的条件下，两名数学科代表也被选中的概率；
②记抽到数学科代表的人数为X，求X的分布列及数学期望E（X）．
下面临界值表仅供参考：

P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k₀	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（其中m为整数），则称m为离实数x最近的整数，记作I[x]，即I[x]=m．设集合A={（x，y）|f（x）=x-I[x]，x∈R}，B={（x，y）|g（x）=log_ax}，其中0＜a＜1，若集合A∩B的元素恰有三个，则a的取值范围为

．

已知复数z满足|z-2-3i|=1，则|z+1+i|的最小值为

．

已知偶函数f（x）是定义在R上的函数，对x∈R都有f（x+6）=f（x）+f（3），若当x∈（-3，-2）时，f（x）=5x，则f（201.5）=

．

已知函数f（x）=aln（x+1）-x²在区间（0，1）内任取两个实数p，q，且p≠q，不等式

试题分类