题目内容
已知偶函数f(x)是定义在R上的函数,对x∈R都有f(x+6)=f(x)+f(3),若当x∈(-3,-2)时,f(x)=5x,则f(201.5)= .
考点:函数的周期性,函数奇偶性的性质,抽象函数及其应用
专题:函数的性质及应用
分析:根据恒等式和偶函数的定义令x=-3代入求出f(3)=0,从而求出函数的周期是6,再利用赋值法进行转化
解答:
解:由题意知,f(x+6)=f(x)+f(3)并且函数是偶函数,
令x=-3代入上式得:f(-3+6)=f(-3)+f(3)=2f(3),
∴f(3)=0
∴f(x+6)=f(x),
∴函数 f(x)的周期是6.
∴f(201.5)=f(34×6-2.5)=f(-2.5)=5×(-2.5)=-12.5,
故答案为:-12.5
令x=-3代入上式得:f(-3+6)=f(-3)+f(3)=2f(3),
∴f(3)=0
∴f(x+6)=f(x),
∴函数 f(x)的周期是6.
∴f(201.5)=f(34×6-2.5)=f(-2.5)=5×(-2.5)=-12.5,
故答案为:-12.5
点评:本题是一道抽象函数问题,题目的设计“小而巧”,解题的关键是巧妙的赋值,利用其奇偶性和所给的关系式得到函数的周期性,再利用周期性求函数值.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
已知命题p:函数y=e|x-1|的图象关于直线x=1对称,q:函数y=cos(2x+
)的图象关于点(
,0)对称,则下列命题中的真命题为( )
| π |
| 6 |
| π |
| 6 |
| A、p∧q | B、p∧¬q |
| C、¬p∧q | D、¬p∨¬q |
 (文)一个用若干块大小相同的立方块搭成的立体图形,主视图和俯视图是同一图形(如图),那么搭成这样一个立体图形最少需要
(文)一个用若干块大小相同的立方块搭成的立体图形,主视图和俯视图是同一图形(如图),那么搭成这样一个立体图形最少需要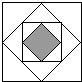 任意画一个正方形,再将这个正方体各边的中点相连得到第二个正方形,依此类推,这样一共画了4个正方形,如图所示.若向图形中随机投一点,则所投点落在第四个正方形的概率是( )
任意画一个正方形,再将这个正方体各边的中点相连得到第二个正方形,依此类推,这样一共画了4个正方形,如图所示.若向图形中随机投一点,则所投点落在第四个正方形的概率是( )