题目内容
已知函数f(x)=aln(x+1)-x2在区间(0,1)内任取两个实数p,q,且p≠q,不等式
>1恒成立,则实数a的取值范围为( )
| f(p+1)-f(q+1) |
| p-q |
| A、[15,+∞) |
| B、(-∞,15] |
| C、(12,30] |
| D、(-12,15] |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:首先,由
的几何意义,得到直线的斜率,然后,得到函数图象上在区间(1,2)内任意两点连线的斜率大于1,从而得到f′(x)=
-2x>1 在(1,2)内恒成立.分离参数后,转化成 a>2x2+3x+1在(1,2)内恒成立.从而求解得到a的取值范围.
| f(p+1)-f(q+1) |
| p-q |
| a |
| x+1 |
解答:
解:∵
的几何意义为:
表示点(p+1,f(p+1)) 与点(q+1,f(q+1))连线的斜率,
∵实数p,q在区间(0,1)内,故p+1 和q+1在区间(1,2)内.
不等式
>1恒成立,
∴函数图象上在区间(1,2)内任意两点连线的斜率大于1,
故函数的导数大于1在(1,2)内恒成立.
由函数的定义域知,x>-1,
∴f′(x)=
-2x>1 在(1,2)内恒成立.
即 a>2x2+3x+1在(1,2)内恒成立.
由于二次函数y=2x2+3x+1在[1,2]上是单调增函数,
故 x=2时,y=2x2+3x+1在[1,2]上取最大值为15,
∴a≥15
∴a∈[15,+∞).
故选A.
| f(p+1)-f(q+1) |
| p-q |
表示点(p+1,f(p+1)) 与点(q+1,f(q+1))连线的斜率,
∵实数p,q在区间(0,1)内,故p+1 和q+1在区间(1,2)内.
不等式
| f(p+1)-f(q+1) |
| p-q |
∴函数图象上在区间(1,2)内任意两点连线的斜率大于1,
故函数的导数大于1在(1,2)内恒成立.
由函数的定义域知,x>-1,
∴f′(x)=
| a |
| x+1 |
即 a>2x2+3x+1在(1,2)内恒成立.
由于二次函数y=2x2+3x+1在[1,2]上是单调增函数,
故 x=2时,y=2x2+3x+1在[1,2]上取最大值为15,
∴a≥15
∴a∈[15,+∞).
故选A.
点评:本题重点考查导数的应用,函数的几何性质等知识,注意分离参数在求解中的灵活运用,属于中档题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知命题p:函数y=e|x-1|的图象关于直线x=1对称,q:函数y=cos(2x+
)的图象关于点(
,0)对称,则下列命题中的真命题为( )
| π |
| 6 |
| π |
| 6 |
| A、p∧q | B、p∧¬q |
| C、¬p∧q | D、¬p∨¬q |
执行如图所示的程序框图,输出的S值是( )


A、-
| ||||
B、
| ||||
| C、0 | ||||
D、
|
设函数f(x)=|lg(x+1)|,满足f(a)=f(-
),f[10(a+1)+6(b+2)-1]=4lg2,其中a,b∈R,且a<b,则a+b的值为( )
| b+1 |
| b+2 |
| A、0 | ||
B、
| ||
C、-
| ||
| D、-1 |
在△ABC中,a=7,b=5,c=3,则cosA等于( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
 (文)一个用若干块大小相同的立方块搭成的立体图形,主视图和俯视图是同一图形(如图),那么搭成这样一个立体图形最少需要
(文)一个用若干块大小相同的立方块搭成的立体图形,主视图和俯视图是同一图形(如图),那么搭成这样一个立体图形最少需要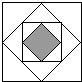 任意画一个正方形,再将这个正方体各边的中点相连得到第二个正方形,依此类推,这样一共画了4个正方形,如图所示.若向图形中随机投一点,则所投点落在第四个正方形的概率是( )
任意画一个正方形,再将这个正方体各边的中点相连得到第二个正方形,依此类推,这样一共画了4个正方形,如图所示.若向图形中随机投一点,则所投点落在第四个正方形的概率是( )