题目内容
9.当点(-6,4)到直线l:(m-2)x-y+2m+2=0的距离最大时m的值为0.分析 求出直线过定点,当点(-6,4)到直线l:(m-2)x-y+2m+2=0的距离最大时,利用斜率的关系,即可求出m的值.
解答 解:由直线l:(m-2)x-y+2m+2=0,可得m(x+2)+(-2x-y+2)=0,
∴x=-2,-2x-y+2=0,
∴x=-2,y=6,即直线过定点(-2,6),
由(-6,4),(-2,6),可得直线的斜率为$\frac{6-4}{-2+6}$=$\frac{1}{2}$,
∴当点(-6,4)到直线l:(m-2)x-y+2m+2=0的距离最大时,直线的斜率为m-2=-2,
∴m=0.
故答案为:0.
点评 本题考查直线方程,考查直线的斜率,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
19.已知α,β分别满足α•lgα=1004,β•10β=1004,则α•β等于( )
| A. | 2$\sqrt{1004}$ | B. | 1004 | C. | 2$\sqrt{2008}$ | D. | 2008 |
14.设点P为有公共焦点F1、F2的椭圆M和双曲线Г的一个交点,且cos∠F1PF2=$\frac{3}{5}$,椭圆M的离心率为e1,双曲线Г的离心率为e2.若e2=2e1,则e1=( )
| A. | $\frac{\sqrt{7}}{5}$ | B. | $\frac{\sqrt{7}}{4}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{10}}{4}$ |
4.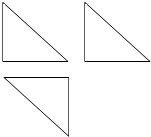 如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )
如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )
 如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )
如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )| A. | 16π | B. | 12π | C. | 8π | D. | 4π |