题目内容
17.若函数f(x)的定义域是[1,3],求下列函数的定义域:(1)f(x2);
(2)f(x+1)-f(2x).
分析 (1)根据函数定义域的求法,直接解不等式1≤x2≤3,即可求函数f(x2)的定义域.
(2)根据函数定义域的求法,直接解不等式1≤x+1≤3,1≤2x≤3,即可求函数f(x+1)-f(2x).的定义域.
解答 解:(1)∵函数y=f(x)的定义域为[1,3],
由1≤x2≤3,得:x∈[-$\sqrt{3}$,-1]∪$[1,\sqrt{3}]$,
故函数y=f(x2)的定义域为[-$\sqrt{3}$,-1]∪$[1,\sqrt{3}]$,
(2)函数f(x)的定义域是[1,3],
可得:1≤x+1≤3并且1≤2x≤3,解得:x∈$[\frac{1}{2},\frac{3}{2}]$.
f(x+1)-f(2x)的定义域为:$[\frac{1}{2},\frac{3}{2}]$.
点评 本题主要考查复合函数定义域的求法,直接利用函数f(x)的定义域,解不等式即可.

练习册系列答案
相关题目
5.方程x2+y2-2x-2y-8=0表示的图形是( )
| A. | 圆 | B. | 一个点 | C. | 两条直线 | D. | 不表示任何图形 |
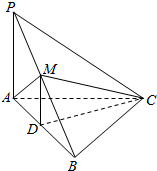 已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.
已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.