题目内容
1.若a,b,c∈(0,+∞),且a+b+c=2,求证:$\sqrt{a+1}$+$\sqrt{b+1}$+$\sqrt{c+1}$<4.分析 根据三维形式的柯西不等式便可得到$[(\sqrt{a+1})^{2}+(\sqrt{b+1})^{2}+(\sqrt{c+1})^{2}][{1}^{2}+{1}^{2}+{1}^{2}]$$≥(\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1})^{2}$,从而便可得到$\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}≤\sqrt{15}$,并且可知当a=b=c=$\frac{2}{3}$时取“=”,从而便可证出$\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}<4$.
解答 证明:根据柯西不等式:
$[(\sqrt{a+1})^{2}+(\sqrt{b+1})^{2}+(\sqrt{c+1})^{2}][{1}^{2}+{1}^{2}+{1}^{2}]$$≥(\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1})^{2}$;
左边=3(a+b+c+3)=15;
∴$\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}≤\sqrt{15}$;
当且仅当$\frac{\sqrt{a+1}}{1}=\frac{\sqrt{b+1}}{1}=\frac{\sqrt{c+1}}{1}$,即a=b=c=$\frac{2}{3}$时取“=”;
∴$\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}≤\sqrt{15}<\sqrt{16}$;
即$\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}<4$.
点评 考查三维形式的柯西不等式公式:$({{a}_{1}}^{2}+{{a}_{2}}^{2}+{{a}_{3}}^{2})({{b}_{1}}^{2}+{{b}_{2}}^{2}+{{b}_{3}}^{2})≥$$({a}_{1}{b}_{1}+{a}_{2}{b}_{2}+{a}_{3}{b}_{3})^{2}$,并且清楚等号成立的条件,放缩法在不等式证明中的应用.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
| A. | 6 | B. | 9 | C. | 7 | D. | 2 |
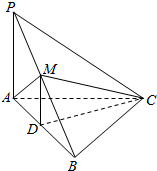 已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.
已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.