题目内容

4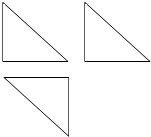．如图，一个几何体的三视图是三个全等的等腰直角三角形，且直角边长为2，则这个几何体的外接球的表面积为（　　）
A．16πB．12πC．8πD．4π

分析 该几何体是一个三棱锥，底面是等腰直角三角形，根据公式求解即可

解答 解：由几何体的三视图知，几何体如图所示的三棱锥，
∵几何体的三视图均为腰长为2的等腰直角三角形，
∴AB=BC=CD=1，且∠ABC=∠BCD=∠ABD=90°，

可以看作是从长方体中截得的一部分，故外接球的直径是长方体的对角线，为2$\sqrt{3}$，
故外接球的表面积为：4$π（\frac{2\sqrt{3}}{2}）^{2}$=12π，
故选：B．

点评 本题考查学生的空间想象能力，分析出几何体是形状是解答的关键，难度不大，是基础题

练习册系列答案
相关题目
11．已知椭圆方程$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），F1、F2是椭圆上的左、右两焦点且在x轴上．
（1）过椭圆的右焦点F1作x轴的垂线交椭圆于P点，点A、B分别是椭圆与x轴负半轴、y轴正半轴的交点，且PF2∥AB，求椭圆的离心率；
（2）过椭圆的右焦点F2作x轴的垂线交椭圆于A、B两点，若$\overline{OA}$•$\overline{OB}$=0求椭圆的离心率．
12．圆x2+y2-6x=0的半径为3．
9．当点（-6，4）到直线l：（m-2）x-y+2m+2=0的距离最大时m的值为0．
16．动圆P和圆C1：（x+1）2+y2=$\frac{1}{4}$外切和圆C2：（x-2）2+y2=$\frac{49}{4}$内切，那么动圆圆心P和已知两圆的圆心C1、C2构成三角形PC1C2的周长等于（　　）
A．5B．6C．7D．8
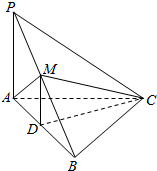9．已知三棱锥P-ABC中，PA⊥平面ABC，底面ABC为边长等于3的正三角形，D、M为AB、PB中点，且△PAM为正三角形．
（1）求证：平面DMC⊥平面PAB；
（2）求点A到平面PBC的距离．
16．已知数列{an}是等比数列，a3=4，且a3是a2+4与a4+14的等差中项；数列{bn}是等差数列，b2=16，其前n项和Tn满足Tn=nλ•bn+1（λ为常数，且λ≠1）．
（1）求数列{an}的通项公式；
（2）求数列{bn}的通项公式及λ的值．
13．已知某程序框图如图所示，则当输入x=1，y=4时，输出的y的值为（　　）
A．6B．9C．7D．2
14．已知抛物线、椭圆和双曲线都经过点M（1，2），它们在x轴上有共同焦点，椭圆的对称轴是坐标轴，抛物线的顶点为坐标原点．则椭圆的长轴长为2+2$\sqrt{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网