题目内容
已知数列{an},a1=1,且满足an=an-1+2n-1(n≥2).
(1)写出数列{an}的前5项;
(2)写出数列{an}的通项公式.
(1)写出数列{an}的前5项;
(2)写出数列{an}的通项公式.
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:(1)根据题意和递推公式依次求出数列{an}的前5项;
(2)由an=an-1+2n-1(n≥2)得an-an-1=2n-1,根据累加法求出数列{an}的通项公式.
(2)由an=an-1+2n-1(n≥2)得an-an-1=2n-1,根据累加法求出数列{an}的通项公式.
解答:
解:(1)由题意得,a1=1,an=an-1+2n-1(n≥2),
所以a2=a1+2×2-1=4,a3=a2+2×3-1=9,a4=a3+2×4-1=16,
a5=a4+2×5-1=25,
所以数列{an}的前5项是1、4、9、16、25;
(2)由an=an-1+2n-1(n≥2)得,an-an-1=2n-1,
则a2-a1=2×2-1,a3-a2=2×3-1,…,an-an-1=2n-1,
以上(n-1)式子相加得,
an-a1=2(2+3+…+n)-(n-1)=2×
-(n-1)
=(n-1)(n+1)=n2-1,
所以an=n2.
所以a2=a1+2×2-1=4,a3=a2+2×3-1=9,a4=a3+2×4-1=16,
a5=a4+2×5-1=25,
所以数列{an}的前5项是1、4、9、16、25;
(2)由an=an-1+2n-1(n≥2)得,an-an-1=2n-1,
则a2-a1=2×2-1,a3-a2=2×3-1,…,an-an-1=2n-1,
以上(n-1)式子相加得,
an-a1=2(2+3+…+n)-(n-1)=2×
| (n-1)(2+n) |
| 2 |
=(n-1)(n+1)=n2-1,
所以an=n2.
点评:本题考查数列的递推公式,以及累加法求数列的通项公式,属于中档题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
已知α∈(0°,45°),且5α的终边上有一点P(sin(-50°),cos130°),则α的值为( )
| A、8° | B、26° |
| C、40° | D、44° |
已知定义在(0,
)上的函数f(x),f′(x)为其导函数,且f(x)<f′(x)•tanx恒成立,则( )
| π |
| 2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、f(1)<2f(
|
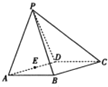 如图,四棱锥P-BCDE中,四边形ABCD为菱形,且∠DAB=60°,△PAD为对边三角形,平面PAD⊥平面ABCD,AB=2,E为AD的中点.
如图,四棱锥P-BCDE中,四边形ABCD为菱形,且∠DAB=60°,△PAD为对边三角形,平面PAD⊥平面ABCD,AB=2,E为AD的中点.(1)求证:AD⊥PB;
(2)求点E到平面PBC的距离.
已知等差数列{an}的前n项和为Sn,若Sn=2,S2n=14,则S4n=( )
| A、68 | B、30 | C、26 | D、16 |
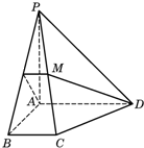 如图,四边形ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AB,M为PC的中点,求证:PB⊥DM.
如图,四边形ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AB,M为PC的中点,求证:PB⊥DM.