题目内容
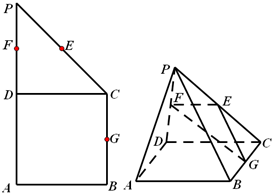 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=CD=PD,E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:PA∥面EFG.
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=CD=PD,E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:PA∥面EFG.考点:直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:证明EF∥平面PAB,同理EG∥平面PAB,从而得到平面PAB∥平面EFG,而PA在平面PAB内,故有PA∥平面EFG.
解答:
证明:∵PE=EC,PF=FD,故EF是△PDC的中位线,∴EF∥CD.
又 CD∥AB,∴EF∥AB,
∴EF∥平面PAB,同理EG∥平面PAB.
∵EF∩EG=E,∴平面PAB∥平面EFG,而PA在平面PAB内,
∴PA∥平面EFG.
又 CD∥AB,∴EF∥AB,
∴EF∥平面PAB,同理EG∥平面PAB.
∵EF∩EG=E,∴平面PAB∥平面EFG,而PA在平面PAB内,
∴PA∥平面EFG.
点评:本题考查证明线面平行的方法,考查直线和平面平行的判定定理的应用,比较基础.

练习册系列答案
相关题目
已知A={x|x>0},B={x|x≤1},则A∩B=( )
| A、{x|x>0} |
| B、{x|x≤1} |
| C、{x|0<x≤1} |
| D、R |
已知定义在(0,
)上的函数f(x),f′(x)为其导函数,且f(x)<f′(x)•tanx恒成立,则( )
| π |
| 2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、f(1)<2f(
|
已知等差数列{an}的前n项和为Sn,若Sn=2,S2n=14,则S4n=( )
| A、68 | B、30 | C、26 | D、16 |
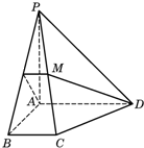 如图,四边形ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AB,M为PC的中点,求证:PB⊥DM.
如图,四边形ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AB,M为PC的中点,求证:PB⊥DM.