题目内容
设
=(
,sina),
=(cosa,
)且
∥
,则锐角a为( )
| a |
| 3 |
| 2 |
| b |
| 1 |
| 3 |
| a |
| b |
| A、30° | B、60° |
| C、45° | D、75° |
考点:二倍角的正弦,平面向量共线(平行)的坐标表示
专题:三角函数的求值,平面向量及应用
分析:直接利用向量的共线的充要条件,列出方程,然后求解即可.
解答:
解:
=(
,sina),
=(cosa,
)且
∥
,
∴sinacosa=
×
=
,∴sin2a=1,∵a是锐角,
所以2a=90°,∴a=45°.
故选:C.
| a |
| 3 |
| 2 |
| b |
| 1 |
| 3 |
| a |
| b |
∴sinacosa=
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
所以2a=90°,∴a=45°.
故选:C.
点评:本题考查向量共线的充要条件的应用,三角函数的化简求值,基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等比数列{an}中,
=2,a4=8,则a6=( )
| a2+a3 |
| a1+a2 |
| A、31 | B、32 | C、63 | D、64 |
设A,B,C为全集R的子集,定义A-B=A∩(∁RB)( )
| A、若A∩B⊆A∩C,则B⊆C |
| B、若A∩B⊆A∩C,则A∩(B-C)=∅ |
| C、若A-B⊆A-C,则B?C |
| D、若A-B⊆A-C,则A∩(B-C)=∅ |
已知A={x|x>0},B={x|x≤1},则A∩B=( )
| A、{x|x>0} |
| B、{x|x≤1} |
| C、{x|0<x≤1} |
| D、R |
直线x+y+1=0的倾斜角为( )
| A、135° | B、120° |
| C、60° | D、45° |
已知α∈(0°,45°),且5α的终边上有一点P(sin(-50°),cos130°),则α的值为( )
| A、8° | B、26° |
| C、40° | D、44° |
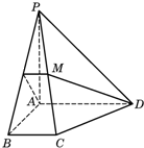 如图,四边形ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AB,M为PC的中点,求证:PB⊥DM.
如图,四边形ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AB,M为PC的中点,求证:PB⊥DM.