题目内容
7. 如图,圆O的弦AB,MN交于点C,且A为弧MN的中点,点D在弧BM上,若∠ACN=3∠ADB,求∠ADB的度数.
如图,圆O的弦AB,MN交于点C,且A为弧MN的中点,点D在弧BM上,若∠ACN=3∠ADB,求∠ADB的度数.
分析 连结AN,DN.利用圆周角定理,结合∠ACN=3∠ADB,求∠ADB的度数.
解答  解:连结AN,DN.
解:连结AN,DN.
因为A为弧MN的中点,所以∠ANM=∠ADN.
而∠NAB=∠NDB,
所以∠ANM+∠NAB=∠ADN+∠NDB,
即∠BCN=∠ADB.
又因为∠ACN=3∠ADB,
所以∠ACN+∠BCN=3∠ADB+∠ADB=180°,
故∠ADB=45°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.

练习册系列答案
相关题目
17.若实数a、b、c∈R+,且ab+ac+bc+2$\sqrt{5}=6-{a^2}$,则2a+b+c的最小值为( )
| A. | $\sqrt{5}-1$ | B. | $\sqrt{5}+1$ | C. | $2\sqrt{5}+2$ | D. | $2\sqrt{5}-2$ |
16.在数列{an}中,a1=2,an+1=an+2,Sn为{an}的前n项和,则S10=( )
| A. | 90 | B. | 100 | C. | 110 | D. | 130 |
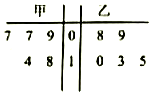 如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.
如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.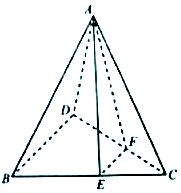 如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.
如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.