题目内容
函数g(x)=x(2-x)的递增区间是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:根据二次函数的图象即可求出其单调增区间.
解答:
解:g(x)=x(2-x)=2x-x2=-(x-1)2+1,
其图象开口向下,对称轴为:x=1,
所以函数的递增区间为:(-∞,1].
故答案为:(-∞,1].
其图象开口向下,对称轴为:x=1,
所以函数的递增区间为:(-∞,1].
故答案为:(-∞,1].
点评:本题考查二次函数的单调性问题,二次函数单调区间一般借助图象求解,主要与二次函数的开口方向与对称轴有关.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
定义在R上的函数满足f(x)=f(x+2),当x∈[1,3]时,f(x)=2-|x-2|,则( )
A、f(sin
| ||||
| B、f (sin1)>f (cos1) | ||||
C、f(cos
| ||||
| D、f (cos2)>f (sin2) |
下列函数中,在区间(0,2)上为增函数的是( )
| A、y=2-x | ||
B、y=
| ||
C、y=-log
| ||
| D、y=-x2+2x+3 |
已知全集U=R,集合A={1,2,3,4,5},B={x∈R|
≤0},则A∩B=( )
| x+2 |
| x-3 |
| A、{1,2} |
| B、{x|-2≤x<3} |
| C、{x|0≤x<3} |
| D、{0,1} |
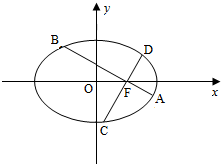 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆