Question

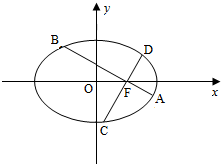如图，在平面直角坐标系xOy中，椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

2

2

，过椭圆右焦点F作两条互相垂直的弦AB与CD．当直线AB斜率为0时，|AB|+|CD|=3

2

．
（Ⅰ）求椭圆的方程；
（Ⅱ）求由A，B，C，D四点构成的四边形的面积的取值范围．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的标准方程

专题：圆锥曲线的定义、性质与方程

分析：（Ⅰ）利用椭圆的离心率，以及，|AB|+|CD|=3

2

．求出a、b，即可求椭圆的方程；
（Ⅱ）①当两条弦中一条斜率为0时，另一条弦的斜率不存在，直接求出面积．
②当两弦斜率均存在且不为0时，设A（x₁，y₁），B（x₂，y₂），且设直线AB的方程为y=k（x-1），与椭圆方程联立，利用韦达定理以及弦长公式，求出AB，CD即可求解面积的表达式，通过基本不等式求出面积的最值．

解答： 解：（Ⅰ）由题意知，e=

c

a

=

2

2

，则a=

2

c，b=c，
∴AB+CD=2a+2

b2

a

=2

2

c+

2

c=3

2

，
所以c=1．所以椭圆的方程为

x2

2

+y2=1．

（Ⅱ）①当两条弦中一条斜率为0时，另一条弦的斜率不存在，
由题意知S四边形=

1

2

AB•CD=

1

2

×2

2

×

2

=2；     
②当两弦斜率均存在且不为0时，设A（x₁，y₁），B（x₂，y₂），
且设直线AB的方程为y=k（x-1），
则直线CD的方程为y=-

1

k

(x-1)．
将直线AB的方程代入椭圆方程中，并整理得（1+2k²）x²-4k²x+2k²-2=0，
所以AB=

k2+1

|x1-x2|=

k2+1

•

2 2 k2+1

1+2k2

=

2 2 (k2+1)

1+2k2

．   
同理，CD=

2 2 ( 1 k2 +1)

1+ 2 k2

=

2 2 (k2+1)

k2+2

． 
所以S四边形=

1

2

•AB•CD=

1

2

•

2 2 (k2+1)

1+2k2

•

2 2 (k2+1)

k2+2

=

4(k2+1)2

2k4+2+5k2

=

4(k+ 1 k )2

2(k+ 1 k )2+1

=2-

2

2(k+ 1 k )2+1

，
∵2(k+

1

k

)2+1≥2(2

k• 1 k

)2+1=9当且仅当k=±1时取等号   
∴S四边形∈[

16

9

，2)
综合①与②可知，S四边形∈[

16

9

，2]

点评：本题考查椭圆方程的求法，直线与椭圆的位置关系的应用，弦长公式的求法以及基本不等式的应用，是综合性比较强的题目．