题目内容
已知函数f(x)=mx+3,g(x)=x2+2x+m,G(x)=f(x)-g(x).
(1)求证:函数G(x)必有零点;
(2)若m=6,试作出函数|G(x)|的简图,并写出它的单调区间;
(3)若函数|G(x)|在[-1,0]上是减函数,求实数m的取值范围.
(1)求证:函数G(x)必有零点;
(2)若m=6,试作出函数|G(x)|的简图,并写出它的单调区间;
(3)若函数|G(x)|在[-1,0]上是减函数,求实数m的取值范围.
考点:函数零点的判定定理,函数的图象
专题:计算题,作图题,函数的性质及应用
分析:(1)化简f(x)-g(x)并令其为零,判断△,从而求证函数G(x)必有零点;
(2)化简|G(x)|=|-x2+4x-3|=|(x-2)2-1|,从而做简图,由图写出单调区间;
(3)G(x)=f(x)-g(x)-1=-x2+(m-2)x+3-m,讨论对称轴从而确定单调性.
(2)化简|G(x)|=|-x2+4x-3|=|(x-2)2-1|,从而做简图,由图写出单调区间;
(3)G(x)=f(x)-g(x)-1=-x2+(m-2)x+3-m,讨论对称轴从而确定单调性.
解答:
(1)证明:∵f(x)-g(x)=-x2+(m-2)x+3-m,令f(x)-g(x)=0,则
∴△=(m-22+4(3-m)=m2-8m+16=(m-4)2≥0,
∴方程f(x)-g(x)=0有实数根,∴函数G(x)=f(x)-g(x)必有零点.
(2)∵m=6,∴|G(x)|=|-x2+4x-3|=|(x-2)2-1|,
令G(x)=0,则x=3或1,
作出y=|G(x)|简图如右图所示.
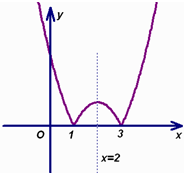
由图可知,单调增区间为:(1,2),(3,+∞);
减区间为:(-∞,1),(2,3).
(3)∵G(x)=f(x)-g(x)-1=-x2+(m-2)x+3-m,
令G(x)=0,则x=1或m-3.
①若m=4,则G(x)=-(x-1)2
∴|G(x)|=(x-1)2在[-1,0]上是减函数,成立.
②若m>4,则m-3>1
|G(x)|=|x2-(m-2)x+m-3|=|(x-1)(x+3-m)|在(-∞,1)上是减函数
∴|G(x)|在[-1,0]上是减函数,成立.
③若m<4,则m-3<1
|G(x)|=|x2-(m-2)x+m-3|=|(x-1)(x+3-m)|在(-∞,m-3),(
,1)上是减函数,
∴m-3≥0或
≤-1,∴m≥3或m≤0,
又m<4,∴3≤m<4或m≤0.
综上,|G(x)|在[-1,0]上是减函数时,m的取值范围是m≤0或m≥3.
∴△=(m-22+4(3-m)=m2-8m+16=(m-4)2≥0,
∴方程f(x)-g(x)=0有实数根,∴函数G(x)=f(x)-g(x)必有零点.
(2)∵m=6,∴|G(x)|=|-x2+4x-3|=|(x-2)2-1|,
令G(x)=0,则x=3或1,
作出y=|G(x)|简图如右图所示.

由图可知,单调增区间为:(1,2),(3,+∞);
减区间为:(-∞,1),(2,3).
(3)∵G(x)=f(x)-g(x)-1=-x2+(m-2)x+3-m,
令G(x)=0,则x=1或m-3.
①若m=4,则G(x)=-(x-1)2
∴|G(x)|=(x-1)2在[-1,0]上是减函数,成立.
②若m>4,则m-3>1
|G(x)|=|x2-(m-2)x+m-3|=|(x-1)(x+3-m)|在(-∞,1)上是减函数
∴|G(x)|在[-1,0]上是减函数,成立.
③若m<4,则m-3<1
|G(x)|=|x2-(m-2)x+m-3|=|(x-1)(x+3-m)|在(-∞,m-3),(
| m-2 |
| 2 |
∴m-3≥0或
| m-2 |
| 2 |
又m<4,∴3≤m<4或m≤0.
综上,|G(x)|在[-1,0]上是减函数时,m的取值范围是m≤0或m≥3.
点评:本题考查了学生的作图能力及函数的零点的判断,属于基础题.

练习册系列答案
相关题目