题目内容
给出以下四个命题:
①若A>B,则cosA<cosB;
②“若a+b≥2,则a,b 中至少有一个不小于1”的逆命题;
③“若x2+y2=0,则x,y都为0”的否命题;
④若x+y≠3,则x≠1或y≠2.
其中真命题是 .
①若A>B,则cosA<cosB;
②“若a+b≥2,则a,b 中至少有一个不小于1”的逆命题;
③“若x2+y2=0,则x,y都为0”的否命题;
④若x+y≠3,则x≠1或y≠2.
其中真命题是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①,若A>B,则cosA<cosB,举例如
>π,则cos
>cosπ,可判断①;
②,写出“若a+b≥2,则a,b 中至少有一个不小于1”的逆命题,可判断②;
③,利用原命题的否命题与其逆命题的等价性可判断③;
④,利用原命题与其逆否命题等价可判断④.
| 5π |
| 3 |
| 5π |
| 3 |
②,写出“若a+b≥2,则a,b 中至少有一个不小于1”的逆命题,可判断②;
③,利用原命题的否命题与其逆命题的等价性可判断③;
④,利用原命题与其逆否命题等价可判断④.
解答:
解:对于①,若A>B,则cosA<cosB,错误,如
>π,但cos
=
>-1=cosπ,故①错误;
对于②,“若a+b≥2,则a,b 中至少有一个不小于1”的逆命题为“a,b 中至少有一个不小于1,则a+b≥2”错误,如a=2>1,b=-1,a+b=1<2,故②错误;
对于③,∵“若x2+y2=0,则x,y都为0”的否命题与其逆命题为等价命题,而其逆命题为“若x,y都为0,则x2+y2=0”为真命题,故③正确;
对于④,∵原命题与其逆否命题真假性一致(等价),
∵命题若x+y≠3,则x≠1或y≠2的逆否命题为:若x=1且y=2,则x+y=3为真命题,
∴若x+y≠3,则x≠1或y≠2为真命题,故④正确.
故答案为:③④.
| 5π |
| 3 |
| 5π |
| 3 |
| 1 |
| 2 |
对于②,“若a+b≥2,则a,b 中至少有一个不小于1”的逆命题为“a,b 中至少有一个不小于1,则a+b≥2”错误,如a=2>1,b=-1,a+b=1<2,故②错误;
对于③,∵“若x2+y2=0,则x,y都为0”的否命题与其逆命题为等价命题,而其逆命题为“若x,y都为0,则x2+y2=0”为真命题,故③正确;
对于④,∵原命题与其逆否命题真假性一致(等价),
∵命题若x+y≠3,则x≠1或y≠2的逆否命题为:若x=1且y=2,则x+y=3为真命题,
∴若x+y≠3,则x≠1或y≠2为真命题,故④正确.
故答案为:③④.
点评:本题考查命题的真假判断与应用,着重考查四种命题之间的关系及真假判断,突出原命题与其逆否命题、原命题的逆命题与其否命题的等价性的考查,属于中档题.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
如果(4x2-
)n的展开式中含有非零常数项,则正整数n的最小值为( )
| 2 |
| x3 |
| A、3 | B、5 | C、6 | D、10 |
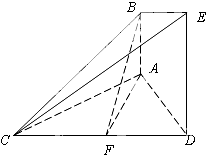 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.