题目内容
已知(
+2x)n展开式中前三项的二项式系数和为37,求n的值.
| 1 |
| 4 |
考点:二项式定理的应用
专题:计算题,二项式定理
分析:由二项式系数的概念,可得:
=37,解得即可得到n.
| C | 0 n |
| +C | 1 n |
| +C | 2 n |
解答:
解:由题意可得:
=37,
化简得1+n+
=37,
解得n=8.
| C | 0 n |
| +C | 1 n |
| +C | 2 n |
化简得1+n+
| n(n-1) |
| 2 |
解得n=8.
点评:本题考查二项式定理的应用,及二项式系数的应用,属于基本题.

练习册系列答案
相关题目
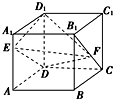 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
圆x2+(y-2)2=1的圆心到直线x+y-1=0的距离为( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、2
|
设某公司原有员工100人从事产品A的生产,平均每人每年创造产值t万元(t为正常数).公司决定从原有员工中分流x(0<x<100)人去进行新开发的产品B的生产.分流后,继续从事产品A生产的员工平均每人每年创造产值在原有的基础上增长了1.2x%.若要保证产品A的年产值不减少,则最多能分流的人数是( )
| A、15 | B、16 | C、17 | D、18 |
若双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相切,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
