题目内容
11.集合$A=\{x|y=\sqrt{2x-{x^2}}\}$,B={y|y=lg(x2+1),y∈Z},则集合A∩B中元素的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 求出集合A,B的等价条件,结合交集的定义进行判断即可.
解答 解:$A=\{x|y=\sqrt{2x-{x^2}}\}$={x|2x-x2≥0}={x|0≤x≤2},
B={y|y=lg(x2+1),y∈Z}={0,1,2,3,…},
则A∩B={0,1,2},共有3个元素,
故选:C
点评 本题主要考查集合的基本运算,根据条件求出集合A,B的等价条件是解决本题的关键.

练习册系列答案
相关题目
19.已知集合A={x|x<a},B={x|x2-3x+2<0},若A∩B=B,则实数a的取值范围是( )
| A. | a≤1 | B. | a<1 | C. | a≥2 | D. | a>2 |
16.在一次实验中,同时抛掷4枚均匀的硬币16次,设4枚硬币正好出现3枚正面向上,1枚反面向上的次数为ξ,则ξ的方差是( )
| A. | 3 | B. | 4 | C. | 1 | D. | $\frac{15}{16}$ |
1.已知抛物线y2=4$\sqrt{3}$x的焦点为F,A、B为抛物线上两点,若$\overrightarrow{AF}$=3$\overrightarrow{FB}$,O为坐标原点,则△AOB的面积为( )
| A. | 8$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
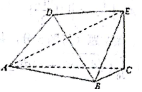 如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.
如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.