题目内容
关于x的方程x2+（a+1）x+a+b+1=0（a≠0，a、b∈R）的两实数根为x1、x2，若0＜x1＜1＜x2，则
的取值范围为 ．
| b |
| a |
考点：简单线性规划的应用,根与系数的关系
专题：函数的性质及应用
分析：先利用二次方程根的分布得出关于a，b的约束条件，再根据约束条件画出可行域，设z=
，再利用z的几何意义求最值，只需求出直线z=
过可行域内的点A或点C时，z分别、取得最小或最大，从而得到
的取值范围．
| b |
| a |
| b |
| a |
| b |
| a |
解答：
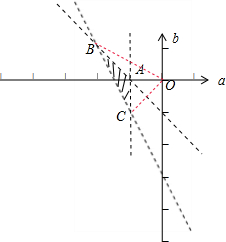解：设f（x）=x2+（a+1）x+a+b+1=0，则由题意可得方程f（x）=0的两实根x1，x2满足0＜x1＜1＜x2的
充要条件是
，即
，画出点（a b）的范围，如图所示：
A（1，0）、B（-2，1）、C（-1，-1）．
而z=
=
表示可行域内的点（a，b）与原点O（0，0）连线的斜率，
故当直线z=
经过点B（-2，1）时，z取得最小值为-
；故当直线z=
经过点C（-1，-1）时，z取得最大值为1，
故z=
的范围为[-
，1]，
故答案为：[-
，1]．
解：设f（x）=x2+（a+1）x+a+b+1=0，则由题意可得方程f（x）=0的两实根x1，x2满足0＜x1＜1＜x2的充要条件是
|
|
A（1，0）、B（-2，1）、C（-1，-1）．
而z=
| b |
| a |
| b-0 |
| a-0 |
故当直线z=
| b |
| a |
| 1 |
| 2 |
| b |
| a |
故z=
| b |
| a |
| 1 |
| 2 |
故答案为：[-
| 1 |
| 2 |
点评：本小题是一道以二次方程的根的分布为载体的线性规划问题，考查化归转化和数形结合的思想，能力要求较高，属于中档题．
练习册系列答案
相关题目
已知直线m，n及平面α，β，下列命题中正确的是（ ）
| A、若m⊥α，n∥β，且m∥n，则α∥β |
| B、若m∥α，n∥β，且m∥n，则α∥β |
| C、若m⊥α，n∥β，且m⊥n，则α⊥β |
| D、若m⊥α，n⊥β，且m⊥n，则α⊥β |
如图，在半径为