题目内容

数列{an}的前n项和Sn，若an=n•n！，求Sn．
考点：数列的求和
专题：等差数列与等比数列
分析：由于an=n•n！=（n+1）!-n!，利用“累加求和”即可得出．
解答： 解：∵an=n•n！=（n+1）!-n!，
∴Sn=（2!-1!）+（3!-2!）+…+[（n+1）!-n!]
=（n+1）!-1！
点评：本题考查了“累加求和”、变形能力，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
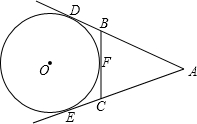如图：AE、AD、BC分别切⊙O于E、D、F，若AD=14，则△ABC的周长为
 
．
数列{an}中，a1=2，an+1=2nan（n∈N*）．
（1）求证：
a1
2
，a2，a3成等比数列；
（2）求{an}的通项公式．
动点M与顶点F1（-5，0），F2（5，0）连线斜率之积为常数p（-1≤p≤0）．求动点M的轨迹方程，指出其轨迹．
已知椭圆
x2
4
+
y2
3
=1，则
y-3
x-1
的取值范围是
 
．
求点A（a，0）到椭圆
x2
2
+y2=1上的点之间的最短距离．
若椭圆2kx2+ky2=1的一个焦点坐标是（0，4），则实数k的值为（　　）
A、
1
8
B、-
1
8
C、
1
32
D、-
1
32
过点（1，-2）且与直线2x-y+1=0垂直的直线l的方程是
 
．
过点（4，-2）斜率为-
3
3
的直线的方程是（　　）
A、
3
x+y+2-4
3
=0
B、
3
x+3y+6-4
3
=0
C、x+
3
y-2
3
-4=0
D、x+
3
y+2
3
-4=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网