题目内容
已知椭圆
+
=1,则
的取值范围是 .
| x2 |
| 4 |
| y2 |
| 3 |
| y-3 |
| x-1 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:令
=t,即有y=tx+3-t,代入椭圆方程
+
=1,消去y,得,关于x的二次方程,由判别式不小于0,解不等式,即可得到所求范围.
| y-3 |
| x-1 |
| x2 |
| 4 |
| y2 |
| 3 |
解答:
解:令
=t,即有y=tx+3-t,
代入椭圆方程
+
=1,消去y,得,
(3+4t2)x2+8t(3-t)x+4(3-t)2-12=0,
由判别式△=64t2(3-t)2-4(3+4t2)[4(3-t)2-12]≥0,
化简,得t2+2t-2≥0,解得t≥
-1或t≤-
-1.
则所求取值范围是(-∞,-
-1]∪[
-1,+∞)
故答案为:(-∞,-
-1]∪[
-1,+∞)
| y-3 |
| x-1 |
代入椭圆方程
| x2 |
| 4 |
| y2 |
| 3 |
(3+4t2)x2+8t(3-t)x+4(3-t)2-12=0,
由判别式△=64t2(3-t)2-4(3+4t2)[4(3-t)2-12]≥0,
化简,得t2+2t-2≥0,解得t≥
| 3 |
| 3 |
则所求取值范围是(-∞,-
| 3 |
| 3 |
故答案为:(-∞,-
| 3 |
| 3 |
点评:本题考查椭圆的方程和运用,考查判别式法求解范围的方法,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知抛物线y2=4x,焦点为P,平面上一定点A(m,0),满足
=2
,过A作直线l,过原点作l的垂线,垂足为Q,则Q的轨迹方程为( )
| OA |
| PA |
| A、y=2x(x≠0) |
| B、x2+y2=1(x≠0) |
| C、(x-1)2+y2=1(y≠0) |
| D、x2-2xy+y2=0(x≠0) |
设等差数列{an}的前n项和为Sn,若
=
,则
=( )
| S5 |
| S10 |
| 1 |
| 3 |
| S5 |
| S20 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线l1的方向向量
=(1.1,1),直线l2的方向向量
=(-2.2,-2),则l1,l2夹角的余弦值为( )
| s1 |
| s2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
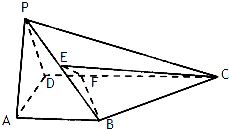 如图,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,△PAD是边长为
如图,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,△PAD是边长为