题目内容
设A=37+C
•35+C
•33+C
•3,B=C
•36+C
•34+C
•32+1,则A-B的值为 .
|
|
|
|
|
|
考点:组合及组合数公式
专题:二项式定理
分析:根据题意,结合二项式定理,得出A-B的值.
解答:
解:∵A=37+C
•35+C
•33+C
•3,B=C
•36+C
•34+C
•32+1,
∴A-B=37-
•36+
•35-
•34+
•33-
•32+
•3-1
=(3-1)7
=128.
故答案为:128.
|
|
|
|
|
|
∴A-B=37-
| C | 1 7 |
| C | 2 7 |
| C | 3 7 |
| C | 4 7 |
| C | 5 7 |
| C | 6 7 |
=(3-1)7
=128.
故答案为:128.
点评:本题考查了二项式定理的应用问题,是基础题目.

练习册系列答案
相关题目
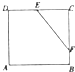 在如图所示的边长为6的正方形ABCD中,点E是DC的中点,且
在如图所示的边长为6的正方形ABCD中,点E是DC的中点,且| CF |
| 2 |
| 3 |
| CB |
| EF |
| AE |
| A、-18 | B、20 |
| C、12 | D、-15 |
已知函数f(2x-1)=3x-4,则f(3)等于( )
| A、-3 | B、-4 | C、1 | D、2 |
设f(x)=
,若f(0)是f(x)的最小值,则a的取值范围是( )
|
| A、[-1,2] |
| B、[-1,0] |
| C、[1,2] |
| D、[0,2] |