题目内容
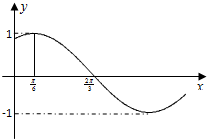
已知函数f(x)是R上的奇函数,对于?x∈(0,+∞)都有f(x+2)=-f(x),且x∈(0,1]时,f(x)=2x+1,则f(-2012)+f(2013)的值为( )
| A、1 | B、2 | C、3 | D、4 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由f(x+2)=-f(x),得到f(x+4)=f(x),即函数的周期是4,利用函数的周期性和奇偶性即可进行求值.
解答:
解:∵f(x+2)=-f(x),
∴f(x+4)=f(x),即函数的周期是4,
∴f(-2012)=f(0)
f(2013)=f(1),
∵f(x)是R上的奇函数,∴f(0)=0,
当x∈(0,1]时,f(x)=2x+1,
∴f(1)=2+1=3,
∴f(-2012)+f(2013)=f(0)+f(1)=3.
故选:C.
∴f(x+4)=f(x),即函数的周期是4,
∴f(-2012)=f(0)
f(2013)=f(1),
∵f(x)是R上的奇函数,∴f(0)=0,
当x∈(0,1]时,f(x)=2x+1,
∴f(1)=2+1=3,
∴f(-2012)+f(2013)=f(0)+f(1)=3.
故选:C.
点评:本题主要考查函数的值的计算,利用条件求出函数的周期性,利用周期性和奇偶性是解决本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知△ABC内一点O满足关系式2
+
+3
=
,则△AOC的面积与△ABC的面积之比为( )
| OA |
| OB |
| OC |
| 0 |
| A、1:6 | B、1:3 |
| C、1:2 | D、5:6 |
设a是函数f(x)=|x2-4|-lnx在定义域内的最小零点,若0<x0<a,则f(x0)的值满足( )
| A、f(x0)>0 |
| B、f(x0)<0 |
| C、f(x0)=0 |
| D、f(x0)的符号不确定 |
已知cos(
-α)=
,
<a<π,则sin(α+
)=( )
| π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
 已知函数
已知函数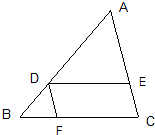 (几何证明选讲选做题)如图,在△ABC中,DE∥BC,DF∥AC,AE=4,EC=2,BC=8,则BF=
(几何证明选讲选做题)如图,在△ABC中,DE∥BC,DF∥AC,AE=4,EC=2,BC=8,则BF=