Question

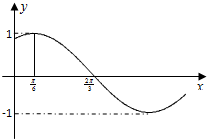已知函数f(x)=Asin(ωx+ϕ)(A＞0，ω＞0，-

π

2

＜ϕ＜

π

2

)，其部分图象如图所示．
（1）求函数 y=f（x）的表达式；
（2）若α∈(-

π

6

，

π

6

)，且f(α)=

3

5

，试求sinα的值．

Answer 1

考点：两角和与差的正弦函数,由y=Asin（ωx+φ）的部分图象确定其解析式

专题：计算题,三角函数的图像与性质

分析：（1）根据函数的最大值，可得A=1．算出周期T=4（

2π

3

-

π

6

）=2π，可得ω=

2π

T

=1．再将(

π

6

，1)代入得到关于ϕ的等式，结合

π

2

＜ϕ＜

π

2

解出ϕ=

π

3

，即可得出函数y=f（x）的表达式；
（2）由（1）得f(α)=sin(α+

π

3

)=

3

5

，利用同角三角函数的关系算出cos(α+

π

3

)=

4

5

，再进行配角：α=（α+

π

3

）-

π

3

，根据两角差的正弦公式加以计算，可得sinα的值．

解答： 解：（1）由图象，可得函数的最大值为A=1，
最小正周期T=4（

2π

3

-

π

6

）=2π，可得ω=

2π

T

=1．
由此可得f（x）=sin（x+ϕ），将(

π

6

，1)代入，
可得sin(

π

6

+ϕ)=1，
∵-

π

2

＜ϕ＜

π

2

，可得-

π

3

＜

π

6

+ϕ＜

2π

3

，
∴

π

6

+ϕ=

π

2

，解得ϕ=

π

3

，
因此，函数y=f（x）的表达式是f(x)=sin(x+

π

3

)，x∈R；
（2）由f(α)=

3

5

，得sin(α+

π

3

)=

3

5

，
∵-

π

6

＜α＜

π

6

，可得

π

6

＜α+

π

3

＜

π

2

，
∴cos(α+

π

3

)=

1-sin2(α+ π 3 )

=

4

5

．
由此可得：

sinα=sin[(α+ π 3 )- π 3 ]=sin(α+ π 3 )cos π 3 -cos(α+ π 3 )sin π 3

=

3 5 × 1 2 - 4 5 × 3 2 = 3 10 - 4 3 10

．

点评：本题给出三角函数的图象，求函数的解析式，并依此求sinα的值．着重考查了由三角函数的部分图象确定其解析式、同角三角函数的基本关系、两角和与差的三角函数公式等知识，属于中档题．