题目内容
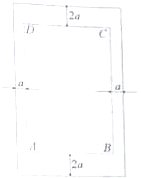 如图为一矩形宣传单,其中矩形ABCD为排版区域,它的左右两边都留有宽为acm的空白,顶部和底部都留有宽为2acm的空白.
如图为一矩形宣传单,其中矩形ABCD为排版区域,它的左右两边都留有宽为acm的空白,顶部和底部都留有宽为2acm的空白.(1)若AB=20cm,BC=30cm,且该宣传单的面积不超过1000cm2,求实数a的取值范围;
(2)若a=1cm,排版区域ABCD的面积为800cm2,应如何设计矩形ABCD的尺寸,才能使矩形宣传单的面积最小?
考点:基本不等式
专题:函数的性质及应用,不等式的解法及应用
分析:解:(1)如图所示,由题意可得:(20+2a)(30+4a)≤1000,又a>0,解出即可;
(2)设AB=xcm,则BC=
cm,设宣传单的面积为S,则S=(x+2)(
+4)=4x+
+808,利用基本不等式解出即可.
(2)设AB=xcm,则BC=
| 800 |
| x |
| 800 |
| x |
| 1600 |
| x |
解答:
解:(1)如图所示,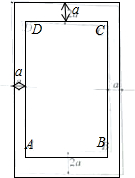 由题意可得:(20+2a)(30+4a)≤1000,
由题意可得:(20+2a)(30+4a)≤1000,
整理得:2a2+35a-100≤0,解得-20≤a≤2.5,
∵a>0,∴0<a≤2.5.
(2)设AB=xcm,则BC=
cm,设宣传单的面积为S,
则S=(x+2)(
+4)=4x+
+808≥2
+808=968.当且仅当x=20cm时取等号.
∴当x=20时,宣传单的面积最小,且为968cm2.
答:(1)实数a取值范围是(0,2.5];
(2)当x=20时,宣传单的面积最小,且为968cm2.
 由题意可得:(20+2a)(30+4a)≤1000,
由题意可得:(20+2a)(30+4a)≤1000,整理得:2a2+35a-100≤0,解得-20≤a≤2.5,
∵a>0,∴0<a≤2.5.
(2)设AB=xcm,则BC=
| 800 |
| x |
则S=(x+2)(
| 800 |
| x |
| 1600 |
| x |
4x•
|
∴当x=20时,宣传单的面积最小,且为968cm2.
答:(1)实数a取值范围是(0,2.5];
(2)当x=20时,宣传单的面积最小,且为968cm2.
点评:本题考查了一元二次不等式的应用、基本不等式的应用,考查了推理能力和计算能力,属于基础题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
已知tanα=2,则
的值为( )
| sin2α-cos2α |
| sinαcosα+2cos2α |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|

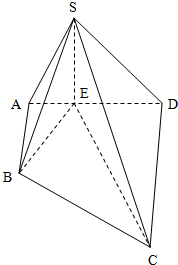 如图,在四棱锥S-ABCD中,AB∥CD,∠BAD=90°,平面SAD⊥平面ABCD,SE⊥AD于点E,CD=DE=2AB=2AE,
如图,在四棱锥S-ABCD中,AB∥CD,∠BAD=90°,平面SAD⊥平面ABCD,SE⊥AD于点E,CD=DE=2AB=2AE,