题目内容
已知函数f(x)=
(x>-1).
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)的最小值.
| ex |
| x+1 |
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)的最小值.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:计算题,导数的概念及应用
分析:(1)根据曲线的解析式求出导函数,把P的横坐标代入导函数中即可求出切线的斜率,根据点的坐标和求出的斜率写出切线的方程即可;
(2)确定函数的单调性,即可求f(x)的最小值.
(2)确定函数的单调性,即可求f(x)的最小值.
解答:
解:(1)∵f(x)=
,
∴f′(x)=
,
∴f′(1)=
,
∵f(1)=
,
∴曲线y=f(x)在点(1,f(1))处的切线方程为ex-4y+e=0;
(2)令f′(x)=0,可得x=0,
x∈(-1,0)时,f′(x)<0,函数单调递减,x∈(0,+∞)时,f′(x)>0,函数单调递增,
∴x=0时,f(x)的最小值为1.
| ex |
| x+1 |
∴f′(x)=
| xex |
| (x+1)2 |
∴f′(1)=
| e |
| 4 |
∵f(1)=
| e |
| 2 |
∴曲线y=f(x)在点(1,f(1))处的切线方程为ex-4y+e=0;
(2)令f′(x)=0,可得x=0,
x∈(-1,0)时,f′(x)<0,函数单调递减,x∈(0,+∞)时,f′(x)>0,函数单调递增,
∴x=0时,f(x)的最小值为1.
点评:此题考查学生会利用导数研究曲线上某点的切线方程,是一道综合题.学生在解决此类问题一定要分清“在某点处的切线”,还是“过某点的切线”;同时解决“过某点的切线”问题,一般是设出切点坐标解决.

练习册系列答案
相关题目
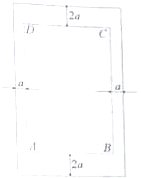 如图为一矩形宣传单,其中矩形ABCD为排版区域,它的左右两边都留有宽为acm的空白,顶部和底部都留有宽为2acm的空白.
如图为一矩形宣传单,其中矩形ABCD为排版区域,它的左右两边都留有宽为acm的空白,顶部和底部都留有宽为2acm的空白.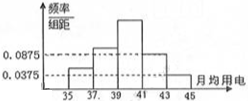 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图.其中直方图从左到右前3个小矩形的面积之比为1:2:3.
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图.其中直方图从左到右前3个小矩形的面积之比为1:2:3.