题目内容
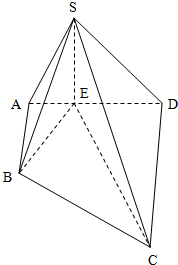 如图,在四棱锥S-ABCD中,AB∥CD,∠BAD=90°,平面SAD⊥平面ABCD,SE⊥AD于点E,CD=DE=2AB=2AE,
如图,在四棱锥S-ABCD中,AB∥CD,∠BAD=90°,平面SAD⊥平面ABCD,SE⊥AD于点E,CD=DE=2AB=2AE,(1)证明:平面SBE⊥平面SEC;
(2)若SE=BE,求直线CE与平面SBC所成角的正弦值.
考点:平面与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)由已知条件推导出∠AEB=∠ABE=45°,∠DEC=∠DCE=45°,从而得到CE⊥BE,又由∠SE⊥AD,得到SE⊥CE,进而得到CE⊥平面SAE,由此能证明平面SBE⊥平面SEC.
(2)以E为原点,EB、EC、ES分别为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能求出直线CE与平面SBC所成角的正弦值.
(2)以E为原点,EB、EC、ES分别为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能求出直线CE与平面SBC所成角的正弦值.
解答:
(1)证明:CD=DE=2AB=2AE,∠BAD=90°,AB∥CD,
∴∠CDE=90°,且∠AEB=∠ABE=45°,
同理∠DEC=∠DCE=45°,
∴∠BEC=90°,即CE⊥BE,
又∵平面CAD⊥平面ABCD,
∴∠SE⊥AD,平面ABCD∩平面SAD=AD,CE?平面ABCD,
∴SE⊥CE,又∵SE∩BE=E,∴CE⊥平面SAE,
又∵CE?平面SEC,∴平面SBE⊥平面SEC.
(2)以E为原点,EB、EC、ES分别为x轴、y轴、z轴,
建立空间直角坐标系,
设CD=DE=2AB=2AE=2,且SE=BE=
,
则C(0,2
,0),B(
,0,0),S(0,0,
),E(0,0,0),
∴
=(-
,2
,0),
=(
,0,-
),
=(0,-2
,0),
设平面SBC的一个法向量为
=(x,y,z),
则
,取x=
,得
=(
,
,
),
设直线CE与平面SBC所成角为θ,
则sinθ=|cos<
,
>|=|
|=
.
∴直线CE与平面SBC所成角的正弦值是
.
∴∠CDE=90°,且∠AEB=∠ABE=45°,
同理∠DEC=∠DCE=45°,
∴∠BEC=90°,即CE⊥BE,
又∵平面CAD⊥平面ABCD,
∴∠SE⊥AD,平面ABCD∩平面SAD=AD,CE?平面ABCD,
∴SE⊥CE,又∵SE∩BE=E,∴CE⊥平面SAE,
又∵CE?平面SEC,∴平面SBE⊥平面SEC.

(2)以E为原点,EB、EC、ES分别为x轴、y轴、z轴,
建立空间直角坐标系,
设CD=DE=2AB=2AE=2,且SE=BE=
| 2 |
则C(0,2
| 2 |
| 2 |
| 2 |
∴
| BC |
| 2 |
| 2 |
| SB |
| 2 |
| 2 |
| CE |
| 2 |
设平面SBC的一个法向量为
| n |
则
|
| 2 |
| n |
| 2 |
| 1 | ||
|
| 2 |
设直线CE与平面SBC所成角为θ,
则sinθ=|cos<
| n |
| CE |
(-2
| ||||||||
|
| 1 |
| 3 |
∴直线CE与平面SBC所成角的正弦值是
| 1 |
| 3 |
点评:本题考查平面与平面垂直的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
已知sinα>0,cosα>0,则角α的终边落在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
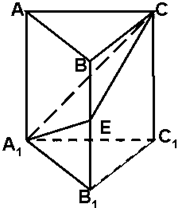 如图,在正三棱柱ABC-A1B1C1中,E为BB1的中点,求证:截面A1EC⊥侧面AC1.
如图,在正三棱柱ABC-A1B1C1中,E为BB1的中点,求证:截面A1EC⊥侧面AC1.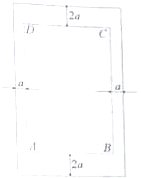 如图为一矩形宣传单,其中矩形ABCD为排版区域,它的左右两边都留有宽为acm的空白,顶部和底部都留有宽为2acm的空白.
如图为一矩形宣传单,其中矩形ABCD为排版区域,它的左右两边都留有宽为acm的空白,顶部和底部都留有宽为2acm的空白.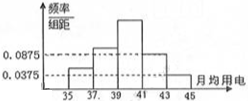 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图.其中直方图从左到右前3个小矩形的面积之比为1:2:3.
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图.其中直方图从左到右前3个小矩形的面积之比为1:2:3.