题目内容
从某校高三年级学生一次数学测试的400份试卷中随机抽取若干份试卷作为样本进行分析评估，抽取的试卷成绩的茎叶图和频率分布直方图都都受到了不同程度的损坏，其可见部分如下，据此解答下列问题：
（Ⅰ）求抽取的成绩在[80，90）的试卷份数及样本数据的中位数；
（Ⅱ）若样本数据中得分在[80，90）的数学成绩的平均分为85，估计该校高三年级学生此次数学测试的平均成绩．
（Ⅰ）求抽取的成绩在[80，90）的试卷份数及样本数据的中位数；
（Ⅱ）若样本数据中得分在[80，90）的数学成绩的平均分为85，估计该校高三年级学生此次数学测试的平均成绩．
考点：茎叶图,众数、中位数、平均数
专题：概率与统计
分析：（Ⅰ）抽取的成绩在[50，60）的试卷份数是2份，频率是0.01×1=0.1，由此能求出一共抽取了20份试卷，从而能求出结果．
（Ⅱ）利用平均数公式计算．
（Ⅱ）利用平均数公式计算．
解答：
解：（Ⅰ）∵抽取的成绩在[50，60）的试卷份数是2份，频率是0.01×1=0.1，
∴一共抽取了
=20人．
∴抽取的成绩在[80，90）的试卷份数为：20-2-4-8-2=4份，
样本数据的中位数是
=74．
（Ⅱ）
=
（100+240+560+85×4+180+6+8+2+3+5+8+1+2+2+3+5+6+7+8+5+8）=74.95．
∴一共抽取了
| 2 |
| 0.1 |
∴抽取的成绩在[80，90）的试卷份数为：20-2-4-8-2=4份，
样本数据的中位数是
| 73+75 |
| 2 |
（Ⅱ）
. |
| x |
| 1 |
| 20 |
点评：本题考查频率分布直方图的应用，解题时要认真审题，是基础题．
练习册系列答案
相关题目
若函数f（x）是奇函数，且在区间[-
，0]内单调递减，则f（x）可以是（ ）
| π |
| 2 |
| A、-sinx | B、-cosx |
| C、sinx | D、cosx |
任意向量
=（a1，a2），
=（b1，b2），定义运算?：
?
=（a2b2，a1b1），下列等式中（“+”和“•”是通常的向量加法和数量积，λ∈R），不恒成立的是（ ）
| a |
| b |
| a |
| b |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、（λ
| ||||||||||||||
D、
|
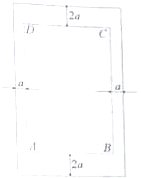如图为一矩形宣传单，其中矩形ABCD为排版区域，它的左右两边都留有宽为acm的空白，顶部和底部都留有宽为2acm的空白．