题目内容
已知复数z1=1+i，z2=m-i（m∈R，i是虚数单位），若z1•z2为纯虚数，则m= ．
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用两个复数代数形式的乘除法法则化简z1•z2 ，再根据z1•z2为纯虚数，它的实部等于零且虚部不等于零，求得m的值．
解答：
解：根据题意可得z1•z2 =（1+i）（m-i）=m+1+（m-1）i 是纯虚数，
∴m+1=0，且 m-1≠0，求得 m=-1，
故答案为：-1．
∴m+1=0，且 m-1≠0，求得 m=-1，
故答案为：-1．
点评：本题主要考查复数的基本概念，两个复数代数形式的乘除法法则的应用，虚数单位i的幂运算性质，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
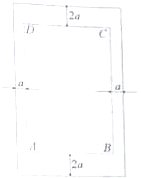如图为一矩形宣传单，其中矩形ABCD为排版区域，它的左右两边都留有宽为acm的空白，顶部和底部都留有宽为2acm的空白．
等差数列{an}中，a1=1，a3=4，则公差d等于（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|