题目内容
已知函数f（x）=ax3+bx2-3x在x=±1处取得极值．
（1）求a，b
（2）讨论f（1）和f（-1）是函数f（x）的极大值还是极小值；
（3）过点A（0，16）作曲线y=f（x）的切线，求此切线方程．
（1）求a，b
（2）讨论f（1）和f（-1）是函数f（x）的极大值还是极小值；
（3）过点A（0，16）作曲线y=f（x）的切线，求此切线方程．
考点：利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题：综合题,导数的综合应用
分析：（1）利用极值的意义，建立方程，即可求a，b；
（2）确定函数的单调性，即可判断f（1）和f（-1）是函数f（x）的极大值还是极小值；
（3）设切点坐标．利用导数的几何意义求切线方程，然后利用切线过原点，确定切点坐标即可．
（2）确定函数的单调性，即可判断f（1）和f（-1）是函数f（x）的极大值还是极小值；
（3）设切点坐标．利用导数的几何意义求切线方程，然后利用切线过原点，确定切点坐标即可．
解答：
解：（1）f'（x）=3ax2+2bx-3，
依题意，f'（1）=f'（-1）=0，即
解得a=1，b=0．
（2）f（x）=x3-3x，f'（x）=3x2-3=3（x+1）（x-1）．
令f'（x）=0，得x=-1，x=1．
若x∈（-∞，-1）∪（1，+∞），则f'（x）＞0，故f（x）在（-∞，-1）上是增函数，f（x）在（1，+∞）上是增函数．
若x∈（-1，1），则f'（x）＜0，故f（x）在（-1，1）上是减函数．
所以，f（-1）=2是极大值；f（1）=-2是极小值．
（3）曲线方程为y=x3-3x，点A（0，16）不在曲线上．
设切点为M（x0，y0），则点M的坐标满足y0=
-3x0．
因f′(x0)=3(
-1)，故切线的方程为y-y0=3(
-1)(x-x0)
注意到点A（0，16）在切线上，有16-(
-3x0)=3(
-1)(0-x0)化简得
=-8，解得x0=-2．
所以，切点为M（-2，-2），切线方程为9x-y+16=0．
依题意，f'（1）=f'（-1）=0，即
|
解得a=1，b=0．
（2）f（x）=x3-3x，f'（x）=3x2-3=3（x+1）（x-1）．
令f'（x）=0，得x=-1，x=1．
若x∈（-∞，-1）∪（1，+∞），则f'（x）＞0，故f（x）在（-∞，-1）上是增函数，f（x）在（1，+∞）上是增函数．
若x∈（-1，1），则f'（x）＜0，故f（x）在（-1，1）上是减函数．
所以，f（-1）=2是极大值；f（1）=-2是极小值．
（3）曲线方程为y=x3-3x，点A（0，16）不在曲线上．
设切点为M（x0，y0），则点M的坐标满足y0=
| x | 3 0 |
因f′(x0)=3(
| x | 2 0 |
| x | 2 0 |
注意到点A（0，16）在切线上，有16-(
| x | 3 0 |
| x | 2 0 |
| x | 3 0 |
所以，切点为M（-2，-2），切线方程为9x-y+16=0．
点评：本题主要考查函数的单调性与极值，考查导数的几何意义，要注意过点的切线和在点处的切线的不同．
练习册系列答案
相关题目
设ω∈（0，10]，则函数y=sinωx在区间（-
，
）上是增函数的概率是（ ）
| π |
| 3 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
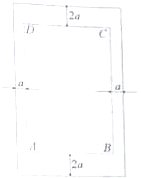如图为一矩形宣传单，其中矩形ABCD为排版区域，它的左右两边都留有宽为acm的空白，顶部和底部都留有宽为2acm的空白．