题目内容
图中,可表示函数y=f(x)的图象的只可能是( )
A、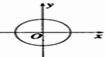 |
B、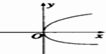 |
C、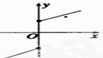 |
D、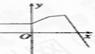 |
考点:函数的概念及其构成要素
专题:函数的性质及应用
分析:根据函数的定义进行判断.主要是利用从自变量x到函数值y的对应为一对一或多对一的关系,而不可出现一对多的情况,由此对四个选项逐个判断.
解答:
解:对于A,B,显然出现了二对一的情况.故不满足函数定义,故A,B错误;
对于C,当x=0时,对应两个y值,故C错误.
对于D,显然满足函数的定义.
故选D
对于C,当x=0时,对应两个y值,故C错误.
对于D,显然满足函数的定义.
故选D
点评:本题考查了函数的对应定义,主要是必须要满足一对一或多对一的关系.而不能出现一对多的情况.

练习册系列答案
相关题目
设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(2)=( )
| A、6 | B、-6 | C、10 | D、-10 |
命题“对任意的x∈R,x2+1>0”的否定是( )
| A、不存在x∈R,x2+1>0 |
| B、存在x∈R,x2+1>0 |
| C、存在x∈R,x2+1≤0 |
| D、对任意的x∈R,x2+1≤0 |
已知函数f(x)的导函数f′(x),满足xf′(x)+2f(x)=
,且f(1)=1,则函数f(x)的最大值为( )
| 1 |
| x2 |
| A、0 | ||
B、
| ||
C、
| ||
| D、2e |