题目内容
已知函数f(x)的导函数f′(x),满足xf′(x)+2f(x)=
,且f(1)=1,则函数f(x)的最大值为( )
| 1 |
| x2 |
| A、0 | ||
B、
| ||
C、
| ||
| D、2e |
考点:导数的运算,函数的最值及其几何意义
专题:导数的概念及应用
分析:由题意构造函数g(x)=x2f(x),可解得g(x)=1+lnx,f(x)=
,利用导数判断函数f(x)的单调性,求得最大值即可.
| 1+lnx |
| x2 |
解答:
解:∵xf′(x)+2f(x)=
,
∴x2f′(x)+2xf(x)=
,
令g(x)=x2f(x),则g′(x)=x2f′(x)+2xf(x)=
,
∵f(1)=1,∴g(1)=1,
∴g(x)=1+lnx,f(x)=
,∴f′(x)=
,
∴x<e-
时,f′(x)=
>0,x>e-
时,f′(x)=
<0,
∴当x=e-
时,f(x)max=f(e-
)=
=
.
故选C.
| 1 |
| x2 |
∴x2f′(x)+2xf(x)=
| 1 |
| x |
令g(x)=x2f(x),则g′(x)=x2f′(x)+2xf(x)=
| 1 |
| x |
∵f(1)=1,∴g(1)=1,
∴g(x)=1+lnx,f(x)=
| 1+lnx |
| x2 |
| -1-2lnx |
| x3 |
∴x<e-
| 1 |
| 2 |
| -1-2lnx |
| x3 |
| 1 |
| 2 |
| -1-2lnx |
| x3 |
∴当x=e-
| 1 |
| 2 |
| 1 |
| 2 |
1+lne-
| ||
(e-
|
| e |
| 2 |
故选C.
点评:本题主要考查利用导数研究函数的性质,解题的关键是构造函数g(x)=x2f(x),逻辑性较强,属于中档题.

练习册系列答案
相关题目
图中,可表示函数y=f(x)的图象的只可能是( )
A、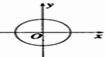 |
B、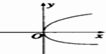 |
C、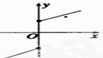 |
D、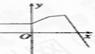 |
若f(x)=x2-2(a-1)x+2在(-∞,3]上是减函数,则a的取值范围是( )
| A、a>4 | B、a<4 |
| C、a≥4 | D、a≤4 |
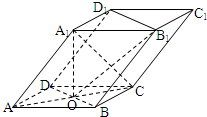 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=