题目内容
已知函数y=f(x)是定义域为R的指数函数.
(Ⅰ)若f(2)=
,求函数f(x)的解析式;
(Ⅱ)若f(x0)=8,求f(
x0)的值;
(Ⅲ)若f(x)在区间[0,+∞)上的值域是(0,1],且f(2x2-3x+1)≤f(x2+2x-5),求实数x的取值范围.
(Ⅰ)若f(2)=
| 1 |
| 4 |
(Ⅱ)若f(x0)=8,求f(
| 1 |
| 2 |
(Ⅲ)若f(x)在区间[0,+∞)上的值域是(0,1],且f(2x2-3x+1)≤f(x2+2x-5),求实数x的取值范围.
考点:函数单调性的性质,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(Ⅰ)先设出函数的表达式,由f(2)=
,代入求出a的值即可;
(Ⅱ)根据f(
x0)=a
x0=(ax0)
=8
=
=2
,从而得到答案;
(Ⅲ)结合函数的单调性,得到不等式2x2-3x+1≥x2+2x-5,解出即可.
| 1 |
| 4 |
(Ⅱ)根据f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 2 |
(Ⅲ)结合函数的单调性,得到不等式2x2-3x+1≥x2+2x-5,解出即可.
解答:
解:设f(x)=ax(a>0,且a≠1),
(Ⅰ)因为f(2)=
,
所以a2=
,所以a=
所以函数f(x)的解析式的解析式为f(x)=(
)x;
(Ⅱ)因为f(x0)=8,所以ax0=8,
所以f(
x0)=a
x0=(ax0)
=8
=
=2
;
(Ⅲ)因为f(x)是指数函数,且在区间[0,+∞)上的值域是(0,1],
所以0<a<1,
所以f(x)在R上是单调递减函数,
又因为f(2x2-3x+1)≤f(x2+2x-5),
所以2x2-3x+1≥x2+2x-5
所以x2-5x+6≥0
所以x≤2,或x≥3
故实数x的取值范围是{x|x≤2,或x≥3}.
(Ⅰ)因为f(2)=
| 1 |
| 4 |
所以a2=
| 1 |
| 4 |
| 1 |
| 2 |
所以函数f(x)的解析式的解析式为f(x)=(
| 1 |
| 2 |
(Ⅱ)因为f(x0)=8,所以ax0=8,
所以f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 2 |
(Ⅲ)因为f(x)是指数函数,且在区间[0,+∞)上的值域是(0,1],
所以0<a<1,
所以f(x)在R上是单调递减函数,
又因为f(2x2-3x+1)≤f(x2+2x-5),
所以2x2-3x+1≥x2+2x-5
所以x2-5x+6≥0
所以x≤2,或x≥3
故实数x的取值范围是{x|x≤2,或x≥3}.
点评:本题考查了函数的单调性,考查了考查了求指数函数的表达式,是一道中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
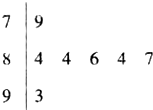 如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )
如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )| A、86,84 |
| B、84,84 |
| C、85,84 |
| D、85,93 |
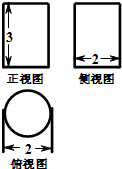 如图,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )
如图,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )| A、7π | B、8π |
| C、10π | D、π+12 |
若函数f(x)与函数g(x)=2x互为反函数,且f(a)+f(b)=4,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
给出如下性质:①最小正周期为π;②图象关于直线x=
对称;③在(-
,
)上是增函数.则同时具有上述性质的一个函数是( )
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
A、y=sin(
| ||||
B、y=cos(
| ||||
C、y=sin(2x-
| ||||
D、y=cos(2x+
|
图中,可表示函数y=f(x)的图象的只可能是( )
A、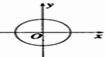 |
B、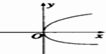 |
C、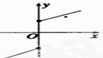 |
D、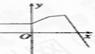 |